FRIプロトコルを用いたSTARKアルゴリズムの紹介

Table of Contents

概要

STARK(Scalable Transparent ARguments-of-Knowledge)とは、以下を満たすような証明システムである。

Scalable ... 以下の2つを意味する。
- 証明者の証明にかかる時間（証明時間）が証明したいステートメントをそのまま実行したときの時間（実行時間）に対して、ほぼ線形である。
- 検証者の検証にかかる時間（検証時間）が検証したいステートメントの実行時間tに対して $O(\text{poly}(\text{log}(t))$ である。
Transparent ... トラステッドセットアップが存在しない。
Arguments of Knowledge ... 証明者の能力が確率的多項式時間チューリングマシンに制限された証明システムである。

これを実現するための概要は以下の通りである。

証明したいプログラムのすべての実行履歴（メモリの状態）をテーブルに書き出し、そのテーブルを多項式補間して表現する（Algebraic Intermediate Representation; AIR)
多項式表現f(x)が特定の点aで0として評価されるとき f(x)は(x-a)で割り切れる。同様にしてfが他の実行履歴の条件に対応したn個の点で割り切れるならば、証明者はfを割り切ることでd = (deg(f) - n)次以下の多項式q(x)を作ることができる。
証明者がd次以下のq(x)のような多項式を知っているということを検証者がFRI(Fast Reed-Solomon IOP)プロトコルを用いて検証する
証明者が知識を証明した多項式と接続する境界条件(プログラムの初期状態、終了状態)についても知識証明を行う。

基本的に(2)までは問題の形式を変換しているだけだが、(3)において検証者が少ない回数のオラクル問い合わせを証明者に対して行いながら、問題ステートメントが正しいことを検証することになる。
プログラム実行履歴の全体を見ずに部分を見ただけで、全体の正しさがわかるというのは不思議な感じがするが、符号理論におけるチェックサムのようなものと考えれば良い。

実際、この記事で解説するFRI(Fast Reed-Solomon IOP)プロトコルではリード・ソロモンという名前が入っているが、ここでいうリード・ソロモン符号[10][11][12][13][21]は「多項式の評価値の列をコミットして使う」という以上の意味はない。

STARKが多くのSNARK実装と比べて優れている点として、ハッシュ関数の存在以外には暗号学的な仮定を必要としないという点がある。

FRIプロトコル

FRIプロトコルとは「ある関数が低次多項式で表現できるか（どのくらい低次多項式に似ていて見分けがつかないか）」を表すための判定アルゴリズムである。

単純な低次テスト

有限体F上の係数と変数を持つ関数fを考える。証明者は関数fの実体を持っているが、検証者は持っていない。このため、検証者はfの点の値を知りたい時、証明者にオラクル問い合わせをしなければならない。

今、証明者が関数fが確実にd次以下の次数を持つ多項式であると主張したいならば、F上のすべての点に対するfの評価値を検証者に送信する必要がある。なぜならば、例えばfはただ一点を除いてd次以下の多項式と一致し、一点でのみ多項式とずれている可能性があるからである。このような状況ではfが確実に多項式であるかどうかを知る効率的な方法は存在しない。

しかし、f上のランダムな点を問い合わせてそれらの関係に矛盾がないかチェックすることで、確率的に多項式であろうと推測することは可能である。

以下の方法で、ある関数fがd次以下の低次多項式であるかどうかを確率的にテストすることができる。

$\mathbb{F}_q$ からd+2個の相異なる点 $x_0, ..., x_{d+1}$ をランダムに選ぶ。その後、 $f$ に対してd+2個の点の評価を行い、選んだ点をすべて満たすd次以下の多項式があるかどうかを調べる。そのような多項式が存在すれば受理し、そうでなければ拒否する。

このテストはd+2箇所で関数fを評価しているので、クエリ複雑性がd+2であるといえる。

低次テストのFRIへの拡張

上記の低次テストはクエリ複雑性が d+2 のものであった。O(d)よりも小さいクエリ複雑性を持つような低次テストは存在するだろうか？
証明者側と協力することによって、これまで「低次多項式との近似性のテスト」と類似のプロトコルである「低次多項式との近似性の対話的証明」を実行することができる。リード・ソロモン符号を使った近似性の対話的証明では、合計でO(log(d))程度のクエリ複雑性で実行することができる。

FRI（Fast Reed-Solomon IOP）プロトコルとは、この近似性の証明にほかならない。
FRIを説明する前に、IOPとは何かを説明しておこう。

IOP (Interactive Oracle Proof; 対話型オラクル証明)

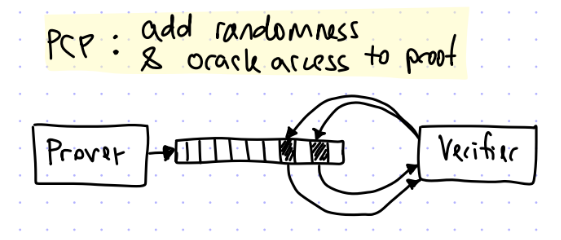
IOPとは何かを説明する前に、PCP[4]における証明が何だったのかを思い出す。以下画像は[3]より転載。

PCPは、証明者の持っている答えのうちランダムな箇所を検証者が覗き見る（オラクル問い合わせ）ことによって、少ない回数のやりとりで証明者が検証者を納得させられるようなプロトコルであった。
証明者はまず答えのリストをコミットしておき、検証者はランダムに選んだ答えの箇所が確かに事前にコミットされたものであることを確認する。このコミットは一度だけ行われる。

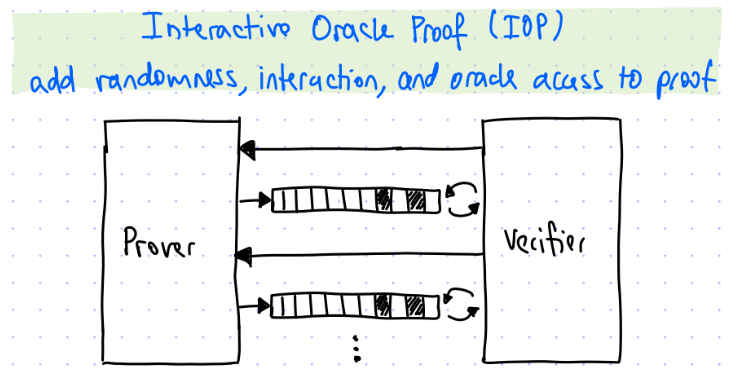
IOPではPCPを更に一般化している。IOPではPCPと同様のコミットメント・オラクル問い合わせを行った後、検証者は再度証明者との対話が可能であり、その対話の結果としてまた証明者が新たなオラクルテーブルとコミットメントを用意し、検証者はそのオラクルテーブルへの問い合わせを行う。
この証明者との対話と、コミットメント・オラクル問い合わせの繰り返しを許容するのがIOPである。IOPにおいて対話とコミットメント・オラクル問い合わせを一度しか行わない場合は、通常のPCPとなる。

高速フーリエ変換からの類推

高速フーリエ変換で使われる分割統治法のように、低次テストの対象である関数を分解して問題を変形することを考える。
以下、ハット付きの関数は多項式として書き下した関数であり、ハットのついていない関数はオラクルとしてアクセスされる関数であるとする。証明者だけがハット付きの多項式にアクセスでき、検証者は多項式全体を知らない。そのため検証者がある点における関数の値を知りたい場合は、証明者にオラクル問い合わせを行うしかない。

$f: L\rightarrow\mathbb{F},\ \text{deg}(\hat{f}) \lt d$ が次と同値であるようにアルゴリズムを設計したい。
$g,h: L^2 \rightarrow \mathbb{F},\ \text{deg}(\hat{g}), \text{deg}(\hat{h}) \lt d/2$
ここで、多項式の偶数次数項、奇数次数項のみを取り出す関数をeven, oddとし、 $\hat{g} = \text{even}(\hat{f}),\ \hat{h} = \text{odd}(\hat{f})$ と定義し $\hat{f}(x) = \hat{g}(x^2) + x \hat{h}(x^2)$ である。また、ここでは定義域 $L^2$ はLの各要素を有限体上で2乗して(その後modを取って)得られる要素の集合である（ここで2乗してもセキュリティが弱くならないのかは検討の余地あり。2乗すると空間のサイズが約半分になり、より容易に後半の予測ができてしまうようになる気もする）。
すなわち1つの多項式の次数がd以下であることの証明を、2つの多項式の次数がd/2以下であることの証明に変換して、2つ以上の多項式の次数チェックを1回のオラクル問い合わせで行うようにすることができれば、このプロセスを繰り返すことによって次数を指数関数的に小さくしていき、log(d)回程度のオラクル問い合わせによって元のfをテストすることができるようになる。
d+2回ではなくlog(d)回で十分であるのかという点は、IOPによって保証することになる。

2つ以上の多項式の次数チェックを1回で行わないアルゴリズム

まずはじめに、単純なアルゴリズムで、上記の分割を実行した後でg, hのオラクル問い合わせを別々に行うケースを考える。これでは、2分割した後2回のオラクル問い合わせを行うため、問い合わせ回数はO(d)回かかるという問題がある。

すなわち、もとの関数fに対してf, g, h のクエリを実行し、gに対してg, g1, g2のクエリを実行し、hに対してh, h1, h2のクエリを実行する。これをr回繰り返すと、クエリ回数の合計値は $\sum_{i=1}^{r} 2^{i-1} = 2^r - 1$ となる。最終的に多項式の次数は元の次数dとして $d/2^r$ まで落ちるが、最終的な多項式に対してリードソロモン符号によるテストなど、次数に関して線形なクエリ回数が必要なテストを行うと、合計のクエリ回数は $(2^r - 1) \times d/2^r = O(d)$ であり、結局の所問い合わせ回数はそのままリードソロモン符号を使ってクエリした場合と変わらず O(d)となる。

sequenceDiagram
    autonumber
    participant P as 証明者P((F, L, d), f)
    participant V as 検証者V((F, L, d))
    P ->> P: g, hを計算
    P ->> V: g, h: L² → F
    V ->> V: μをランダムに生成しf(μ) ?= g(μ²) + μ h(μ²)を確認

このアルゴリズムのもう一つの問題は、関数fの内部のエラー率(低次多項式から外れている部分の割合)が変化してしまうことにある。
関数 $\hat{g}(x^2), \hat{h}(x^2)$ は偶関数だから、元の関数fではエラーが2箇所あったはずが、1箇所のエラーになってしまう。例えば -1, 1の両方で低次多項式から外れた値になるエラーがあったとき、fではそれが2箇所でエラーとして検出できていたはずなのに、gやhで評価しようとするとはそれらが1箇所でしか検出できない。

従って元の関数が40%のエラー率だったとしても、20%ずつのエラー率を持つ関数のテスト2つに分割されてしまうケースが存在する。もしもその20%のエラーの場所が足し合わせたgとhで同じ場所にマッピングされてしまうと、40%だったエラー率が20%のエラー率に下がってしまうことになる。実際にこのような性質を持つfは存在しているため、どのようなfに対してもエラー率が下がらない方法であるとはいえない。
以下図は[4]より。

したがって、考えられる改良としては

分割した後のオラクル問い合わせ回数は1回にする
内部エラー率を変えない

ような条件を満たす必要がある。2.を解決するために、エラーの発生している多項式を重ね合わせる時には乱数を使い、そのエラーの場所が偶然重なる確率を低くするようにして対処する。それが次に紹介するアルゴリズムである。

検証者が乱数を生成して内部のエラー率を変えないようにするアルゴリズム

gとhを乱数αを使って合成すれば、多項式を変形した時にエラー箇所が一致する確率は小さくなる。

sequenceDiagram
    autonumber
    participant P as 証明者P((F, L, d), f)
    participant V as 検証者V((F, L, d))
    P ->> P: g, hを計算
    V ->> V: αをランダムに生成
    V ->> P: α
    P ->> P: fα := g + α h として定義
    P ->> V: fα:  L² → F
    V ->> V: fα(μ²) ?= g(μ²) + α h(μ²)を確認

この乱数を加える方法ではエラー率を変えずにテストを行うことができるが、クエリ回数はO(log(d))にならない。

FRIプロトコルへの応用

上記のアルゴリズムにおいて関数g,hをfで表現してクエリ回数を削減したものをr回繰り返すことでFRIプロトコルが実現できる。

ランダムなαに対して fを変換する関数をfoldとして定義する。

$\hat{\text{Fold}}(f, \alpha)(x): L^2 \rightarrow \mathbb{F}$ はg, hの代わりにfをそのまま使って以下の通り定義される。
$\hat{\text{Fold}}(f, \alpha)(\gamma^2) := \frac{f(\gamma) + f(-\gamma)}{2} + \alpha \frac{f(\gamma) - f(-\gamma)}{2\gamma}$
このとき、 $\hat{\text{Fold}}(f, \alpha)(x):= \text{even}(\hat{f})(x) + \alpha\ \text{odd}(\hat{f})(x)$ となる。
検証者はFold関数に対して、fを使った間接的な表現をしつつ、かつ任意の点での評価を実行することはできない。Fold関数を任意の点で評価するためには $\hat{f}$ 自体を知らなければならないが、 $\hat{f}$ 自体を知ることができるのは証明者だけである。検証者は最初に選んだ乱数 $\gamma$ に対して $\gamma^2$ という点での値しか知ることができないのだが、FRIプロトコルを実行する上では、この制約の下でも十分である。

このFold関数を使って以下のようにFRIプロトコルを記述する。なお以下図中の 2^r などは $2^r$ を意味する。

sequenceDiagram
    autonumber
    participant P as 証明者P((F, L, d), f₀: L→F)
    participant V as 検証者V((F, L, d))
    V ->> V: μ, α₀, α₁, ..., αᵣ₋₁をランダムに生成
    V ->> P: α₀
    P ->> P: f₁ := Fold(f₀, α₀)
    P ->> V: f₁:  L² → F
    V ->> V: f₁(μ²) ?=  (f₀(μ) + f₀(-μ))/2 + α₀(f₀(μ) - f₀(-μ))/2μを確認
    V ->> P: α₁
    P ->> P: f₂ := Fold(f₁, α₁)
    P ->> V: f₂:  L⁴ → F
    V ->> V: f₂(μ⁴) ?=  (f₁(μ²) + f₁(-μ²))/2 + α₁(f₁(μ²) - f₁(-μ²))/2μ²を確認
    V ->> P: ︙
    P ->> V: ︙
    V ->> P: αᵣ₋₁
    P ->> P: fᵣ := Fold(fᵣ₋₁, αᵣ₋₁)
    P ->> V: fᵣ:  L²^ʳ → F
    V ->> V: fᵣ(μ²^ʳ) ?=  (fᵣ₋₁(μ²^⁽ʳ⁻¹⁾) + fᵣ₋₁(-μ²^⁽ʳ⁻¹⁾))/2 + αᵣ₋₁(fᵣ₋₁(μ²^⁽ʳ⁻¹⁾) - fᵣ₋₁(-μ²^⁽ʳ⁻¹⁾))/2μ²^⁽ʳ⁻¹⁾を確認

このアルゴリズムでは $f_0$ に対して評価される点は $\mu, -\mu$ の2つであり、 $f_1$ に対して評価される点は $\mu^2, -\mu^2$ の2つである。同様にr回実行してもクエリ回数は2r回程度であるから、次数が幾何級数的に減少しても評価点の数は線形でしか増えないことになる。

上図ではIOP部分を簡略化して $f_0(\mu)$ をそのまま評価しているが、実際に最新版のアルゴリズムでは値を評価する前に $f_0(\omega^0), f_0(\omega^1), ..., f_0(\omega^N)$ の値をマークルツリー形式で証明者がコミットしておき(④⑧⑭)、検証者はそのコミットの中からランダムに選んだ引数値 $\omega^i$ を $\mu$ として使い検証を行う[24]。（このコミットメントを作成する際には、fに対して $\omega^{N+1}$ 個の点を評価した列が登場するが、これがリードソロモン符号と同等なものになっているため、FRIプロトコルにはリードソロモンという名前が使われている）

最終的には、十分に次数が落ちると定数関数となる。この定数関数に対して、複数箇所での評価値が正しく定数になるのかどうかをテストすればいい。

このアルゴリズムの複雑性は以下の通り。

証明者の計算時間: $O(|L| + |L|/2 + |L|/4 + ... + |L|/2^{r-1}) = O(|L|)$ 。 $|L| = O(d)$ であり、Foldの計算は与えられた多項式の次数d'に対して項同士を足し合わせる操作がO(d')程度かかる。ただし $r = \text{log}(d)$ かつ $|L| = O(d)$ とする。
検証者の計算時間: $O(r ) = O(\text{log}(d))$ 。r回の検証操作に加えて、最後に定数関数のテストを1回だけ行う。
クエリ複雑性(クエリ回数): $O(r) = O(\text{log}(d))$ 。fを呼び出すのは2r回の点の評価と、最終的定数関数のチェックに対して定数回である。

また、証明の完全性についてはアルゴリズムから必ず成り立つ。健全性については以下の通り。
低次多項式からの距離（類似度）がδである場合、 $\text{max}\{\frac{1}{|\mathbb{F}|}, (1-\delta)^t\}$ であることが示せる。

より大きい上限については $O(\frac{|L|}{|\mathbb{F}|}) + (1 - \text{min}\{\delta, c(\frac{d}{|L|})\})^t$ のようなものが知られている。 $c(\frac{d}{|L|})$ は $\frac{d}{|L|}$ に依存した定数？らしい。

健全性の証明については[5]を参照。

なおこのFRIプロトコルは、検証者が $f_0$ 自体を知らなくても、 $f_0(\mu)$ が本当に正しい関数値の評価になっているということを対話的に検証する（やや不便な）多項式コミットメントスキーム（PCS）の一種になっているとも言える。他のPCSとしてはKZGコミットメント[23]やIPAベースのもの[22]があるが、それらはFRIプロトコルとは違い事前に証明者がコミットメントを作成しておくことができ、かつ任意の点でのコミットメントの公開ができる。
FRIは上記で見たように事前にコミットメントを作ることはできず、(プロトコル上は)対話的にコミットメントを検証するものであり、かつ一度のプロトコルで一箇所でしかコミットメントの検証ができない。

具体例: FRIプロトコルを使ったSTARKアルゴリズム

[6]では、具体的な例を持ち出して特定のプログラムの実行を多項式の条件として変換する方法について書いてある。
例えば、(a)いくつかの数の和が正しいことの証明 (b) 特定のフィボナッチ数列の値が正しく計算されていることの証明 (c)コラッツ数列が1に収束することの証明、などである。

方法としては以下のとおりである。

(i) STARKが満たすべき条件を列挙する。
a. 基本的には初期状態 $A_0$ と終了状態 $A_n$ を持つプログラムのレジスタ状態を管理する。ある状態 $A_i$ が多項式関数の適用によって $A_{i+1}$ という状態に変化する、というものがn回繰り返される計算が「満たすべき条件」である。
b. これらの条件は検証者にも共有されている。FRIプロトコルの中で検証者と共有されずオラクル問い合わせでアクセスされる巨大な関数fは、この実行履歴のドメインすべてを表現するものであり、それぞれの点での評価は過去の実行履歴に依存するため、検証者はこの作用だけを見ても具体的な値を知ることができない。
(ii) 条件を満たすときにだけ次数が一定以下になるような多項式を作る

これらを [6]の記事を元に説明する。

(i)についてはフィボナッチ数列の場合、まず条件を満たすような変数（レジスタ）を以下のように書き表す。

この変数 $A_i$ (ここでは変数一つだけだが、複雑なアルゴリズムでは２つ以上になりうる)が状態の移り変わりによってどのように遷移するかを記したテーブルを考える。
このテーブルがAIRの元になる。証明者はこのテーブルの全体を見ることができるが、検証者は全体をみることができない。

状態番号	変数 $A_i$ の値	関数fと対応付けられる際の引数
0	1	$g^0$
1	1	$g^1$
2	2	$g^2$
3	3	$g^3$
4	5	$g^4$
︙	︙	︙
511	62215	$g^{511}$

それらの変数を多項式の各点における値と対応させて、以下のように多項式fを作る。多項式fは補完によって、最大で511次多項式になることがわかる。

画像の1.,2.,4.の条件式は境界条件(boundary condition)と呼ばれる。境界条件と遷移条件の条件式をまとめて「AIR」(代数的中間表現; algebraic intermediate representation)という。

このような多項式fが満たすべき条件のうち、メインとなる部分は3.である。

次に、(ii)の通り、次数が一定以下になるような多項式に変換する。
画像の3.の条件式(遷移条件; transition condition)をまとめると繰り返し部分を以下のように簡略化できる。多項式の各点において $f(g^2 x) - f(gx) - f(x)$ が0となることから、それらの評価点aに対して(x-a)を因数にもつ。従って以下の商多項式q(x)の分母は割り切れるので次数が一定以下（この場合は 511 - 510 = 1次以下）の多項式になるはずである（なおここでは多項式を位数が512の有限体上での計算としているため、生成元gに対して $g^{512} = g$ となる）。

同様に、1., 2., 4.についてもそれぞれ対応する多項式が得られる。例えば、 1. は $\frac{f(x) -1}{x-1}$ であり、これは (511 - 1 = 510次以下)の多項式になるはずである。

番号	多項式	最大次数
$q_1(x)$	$\frac{f(x) -1}{x-1}$	510
$q_2(x)$	$\frac{f(x) -1}{x-g}$	510
$q_3(x)$	$\frac{f(g^2x) - f(gx) - f(x)}{\prod_{i=0}^{509} (x-g^i) }$	1
$q_4(x)$	$\frac{f(x) -62215}{x-g^{511}}$	510

これらを乱数を使って合成し、511次以下であることが予想される関数q(x)を改めて以下のように書き直す。

$q(x) = \alpha_1 q_1(x) + \alpha_2 q_2(x) + \alpha_3 x^{510} q_3(x) + \alpha_4 q_4(x)$

これによって、少なくとも「フィボナッチ数列の計算過程が正しいことを証明する問題」は「特定の関数q(x)がd以下の次数を持つ多項式であることを証明する問題」に変換できることが直感的に理解できる。q(x)の本体は巨大であり、具体的な多項式は証明者だけが持っている。検証者はq(x)を以下のようなf(x)で表現した式は知っていても、f(x)の個別の値を知らないので、q(x)を評価することはできない。
このような状況で検証者は上で見たようにq(x)上の特定の点を選んでFRIプロトコルのクエリを実行する。
(なお実際にはこのq(x)に対していくつかの点での評価を行って低次であることを調べるが、その際に証明者は以下のように式変形のトリックを使うことで計算量を大幅に減らすことが出来る。)

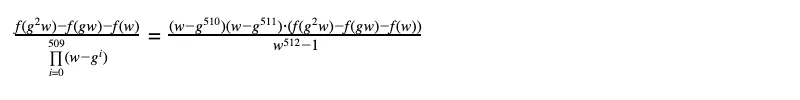
境界条件と遷移条件のそれぞれに対してそれらの間の関係を別途証明[14]することで、全体としての整合性を保つ。

なお、この方法で計算の実行履歴を多項式表現してFRIを実行すると、証明者は(a)正直に実行するため低次多項式を実際に作成しFRIのオラクル問い合わせも矛盾しない、(b)嘘をついて実行するので(高い確率で)低次多項式とはかけ離れた多項式を検証者がランダムに選んだ点で評価することになり嘘が露呈する、の2つの場合にしかなりえない[9]。
したがって、本来は確率的にしか低次多項式かどうかを判定できないFRIプロトコルを用いて、低次多項式を作成できたかどうかを高い精度で判定することができる。

また、ここでは関数fは一つ前の状態から次の状態を計算するために使われているが、STARKにおいては次の状態を計算できなかったとしても、次の状態への遷移が正しい遷移なのかどうかを判定できる多項式であればよいとされる。そのため、状態を計算する関数であればもちろん正しい判定関数なのであるが、状態を計算する関数よりも次数が低い判定関数が存在するならば、そちらを採用することがある。
例えば $p(x) =\{ x^{-1}\ \text{if}\ x \neq 0,\ 0\ \text{otherwise}\}$ のような関数を状態計算関数として多項式表現するとフェルマーの小定理より $f(x) = x^{p-2}$ となるが、計算結果yに対してf(x)=yを満たすかという判定関数の形式で表すと $f(x,y) = (x(xy-1), y(xy-1))$ がすべて0となる(= (0,0))ような入力(x,y)は f(x) = yの条件を満たすと判定できる。状態計算関数は p-2次多項式であり、判定関数は 2つの3次多項式なので大幅に次数を削減できたことになる。

STARK検証者による境界条件の検証

(FRIではなく)STARKプロトコルにおける検証者は、具体的な値としては境界条件のみを知っている状態から、遷移条件を満たす遷移が正しく行われたことを、証明者との対話を通じて知ることになる[16]。

まとめると、やっていることとしては概ね以下のとおりである。

検証者は境界条件と遷移条件を共有している。
検証者は境界条件と遷移条件のコミットメントを証明者から得る。
証明者は境界条件と遷移条件を正しく計算できることをFRIプロトコルで証明する
証明者は遷移条件と境界条件が正しく関係を持っていることを証明する。
以上によって、検証者は証明者が「境界条件から始まり、遷移条件を満たし、境界条件で終わるような実行履歴」を知っているということを納得する。

応用

任意の計算の実行履歴に対して、計算上の制約を多項式で表現できれば、ある条件を満たす計算が行われたことの証明を高速に検証できる。そのため、例えばブロックチェーンの検証（またはその部分的な検証）を高速に行うことができる。
これを利用してZeroSync[8] や Starknet[7][18][19][20] などの開発が行われている。Starknetに関しては参考文献の注も参照。

まとめ

条件を書き下して、有限個の評価点で0になるような形式とし、それを新しい多項式とみなすという手法はplonkを勉強した時にも出てきました。どちらが先かは調べていないので不明です。
もっと深く知りたい場合は、解説付きのpython実装チュートリアルが[15]にあるので、実際に手を動かすことで理解も深まりそうです。
多項式の低次性をテストすることにつなげるのは面白いと思いますが、本当に敵対的な証明者が作った多項式に対して安全なスキームなのかを検証する部分は理論も実装も大変そう[17]なので、安全性の検証が進むことを期待しようと思います。

おまけ

線型性テストと低次多項式テストの代表的なアルゴリズムを解説する。

線型性テスト

n次元の空間において関数fが線形であるとは、n本の基底ベクトルの線型結合としてfが表現できることである。
今、n次元の空間において線形かどうかが不明な関数fがあるとしよう。このfに対して、評価してほしい点xの座標(n個の値からなる組)を送ると、スカラー値f(x)を返してくれる。
ナイーブに考えれば、ランダムな点をたくさん選んでfの評価した値を観測し、それらが同一平面上に存在するならば線形な関数であるとある程度の自信を持って言えるだろう。
しかし、f上のすべての点で値を評価しなければ確実にfが線形かどうかはわからず、従って一つでもf上で評価していない点がある限りfが線形でない可能性は絶えずつきまとうことになる。

このアイデアを一般化して、「どの点を評価したら、どのくらいの確率でfが線形であると言えることになるのか」ということをアルゴリズム化したものがBlum-Luby-Rubinfeldテストである。

Blum-Luby-Rubinfeldテスト

[1]から取ってきた。

アルゴリズム $V_{\text{BLR}}^{f: \mathbb{F}^n \rightarrow \mathbb{F} }$ は 2n個の要素のランダムネスを使い、3箇所のfに対するクエリを実行する。

$x, y \in \mathbb{F}^n$ をランダムに選ぶ。
$f(x) + f(y) = f(x+y)$ であることをテストする。

以下 $\text{LIN}$ は $f: \mathbb{F}^n \rightarrow \mathbb{F}$ なる線形関数の集合とする。

アルゴリズムの完全性: 明らかに $f \in \text{LIN}$ のとき $\forall x,y\in\mathbb{F}^n$ に対して $f(x) + f(y) = f(x+y)$ であるから $\text{Pr}[V_{\text{BLR}}^{f } = 1] = 1$ となる。

アルゴリズムの健全性: $f \notin \text{LIN}$ のとき $\text{Pr}[V_{\text{BLR}}^{f } = 0] \ge \text{min}(\frac{1}{6}, \frac{1}{2}\Delta(f, \text{LIN}))$ である。 $\Delta(f, \text{LIN})$ はfと最も近い線形関数と、fのハミング距離である。詳しくは[1]の証明を参照。直感的には、fが線形に近づくほど判別が難しくなるため健全性の確率の下限が小さくなっていく（下限値が0の時には何の情報も得られない）。またfがどれほど線形から遠かったとしても、健全性の確率の下限が1/6であるから「BLRテストに失敗する確率の下限は1/6」と言える。（ただし上記の確率1/6などは理論的な境界値ではなく、証明の辻褄を合わせるために指定された値である。）

低次テスト(Low-Degree Testing)

[2]を参照。

線型性テストの概念を拡張して、低次テストを考えることができる。すなわち、特定の関数fを何点かで評価して低次多項式で近似できるかどうかを調べるテストである。以下では単変数多項式に対してテストのアルゴリズムを記述しているが、これは多変数多項式に対しても拡張可能である。

単変数多項式に対するRubinfeld-Sudanテスト

$i = 0, ..., d+1$ に対して $c_i = (-1)^{i+1} \begin{pmatrix} d+1 \\ i \end{pmatrix} \in \mathbb{F}_p$ を考える。この $c_i$ に対して以下の補題が成り立つ。

補題

$\forall d \lt p, \forall f: \mathbb{F}_p \rightarrow \mathbb{F}_p$ に対して $f \in \text{F}^{\le d}[x]$ かつそのときのみに限り $\forall a \in \mathbb{F}_p, \sum_{i=0}^{d+1} c_i f(a + i) = 0$

補題の証明は[2]を参照。以上の補題を利用して Rubinfeld-Sudanテストを考える。

アルゴリズム $T^{f: \mathbb{F}_p \rightarrow \mathbb{F}_p }(\mathbb{F}_p, d)$ は 2個の要素のランダムネスを使い、d+2箇所のfに対するクエリを実行する。

$r, s \in \mathbb{F}_p$ をランダムに選ぶ。
fを $r, r+s, r+2s, ..., r+(d+1)s$ でfを評価する。
$\sum_{i=0}^{d+1} c_i \cdot f(r+i s) = 0$ を検証する。

完全性: もしも $f \in \text{F}^{\le d}[x]$ ならば $\text{Pr}_{r,s}[T^f=1] = 1$ である。定義から明らか。

健全性: もしも $f \notin \text{F}^{\le d}[x]$ ならば $\text{Pr}_{r,s}[T^f = 0] \ge \text{min} (\Omega(\frac{1}{d^2}), \frac{1}{2}\Delta(f, \text{F}^{\le d}[x]))$

この健全性の証明については[2]を参照。