拡張紛失通信の基礎: IKNPプロトコルの解説

Table of Contents

はじめに

本稿では¹の論文の解説をします。この論文ではk個の紛失通信プロトコルを利用して、n >> k であるnに対してn個の紛失通信を実行する方法を提案しています。紛失通信プロトコル自体の解説については²を参照して下さい。

プロトコルの解説

今、送信者がn個の値のペア $\mathbf{x} = \{(x_{i,0}, x_{i,1})\}_{i = 1...n}$ を持っているとする。送信者と受信者はn個それぞれのペアのうちどちらか一つを受信者に送る紛失通信プロトコルを実行したい。ここで受信者がi番目の要素として $r_i \in \{0, 1\}$ を選択するものとし、受信者のn個の選択をベクトル $\mathbf{r} = \{r_i\}_{i = 1...n}$ で表す。

普通に考えれば、紛失通信プロトコルをn回並列に実行すれば達成できる。しかし、それでは非効率である。公開鍵暗号と対称鍵暗号を例に挙げると、まず暗号化したいデータを対称鍵で暗号化し、その対称鍵を公開鍵で暗号化するように、コストの低いプロトコルと高いプロトコルを組み合わせて、全体のコストを低く抑える手法が知られている。これと同様のことが紛失通信で実行できないだろうか。

以下のようなIKNPプロトコルでそれが実現できることが知られている。
なお、このIKNPプロトコルでは内部的に受信者と送信者が役割を逆転させた紛失通信プロトコルを実行するが、IKNPプロトコル自体の受信者と送信者という用語をそのまま内部の紛失通信プロトコルにおいても使用する。

以下でkは削減後の紛失通信の数であり、かつセキュリティパラメータでもある。

受信者はランダムな n×k要素の行列 $T \in \{0, 1\}^{n\times k}$ を生成する。また、受信者は $\mathbf{r}$ を持っているのでTのj列 $T^j$ に対して2つの値のタプル $(T^j, T^j \oplus \mathbf{r})$ を生成する。このk組のタプルに対して、以下で送信者が生成したk要素ベクトル $\mathbf{s}$ を使って、内部紛失通信プロトコルを実行する。この内部紛失通信プロトコルは外側のプロトコルと比較したときに、受信者と送信者の役割が逆転していることに注意する。
送信者はランダムなk要素ベクトル\mathbf{s}を生成する。内部紛失通信プロトコルによって新しい行列Q \in \{0, 1\}^{n\times k}を生成する。
1. j列目の列 $T^j$ に対して、 $s_j$ が0の場合 $T^j$ をQのj列とする。
2. j列目の列 $T^j$ に対して、 $s_j$ が1の場合 $T^j \oplus \mathbf{r}$ をQのj列とする。
内部紛失通信プロトコルの結果として入手した行列Qの中身を受信者が知ることは無いが、受信者は（送信者がプロトコルに従っている限りにおいて）以下が成立することを知っている。
1. $r_i = 0$ ならば行列Qのi行目 $Q_i$ は、行列Tのi行目 $T_i$ と一致する。これは、 $r_i = 0$ ならば $\mathbf{s}$ の値にかかわらず列 $T^j$ のもともとの値がQのj列にセットされていることから従う。
2. $r_i = 1$ ならば行列Qのi行目 $Q_i$ は、 $T_i \oplus \mathbf{s}$ と一致する。これは図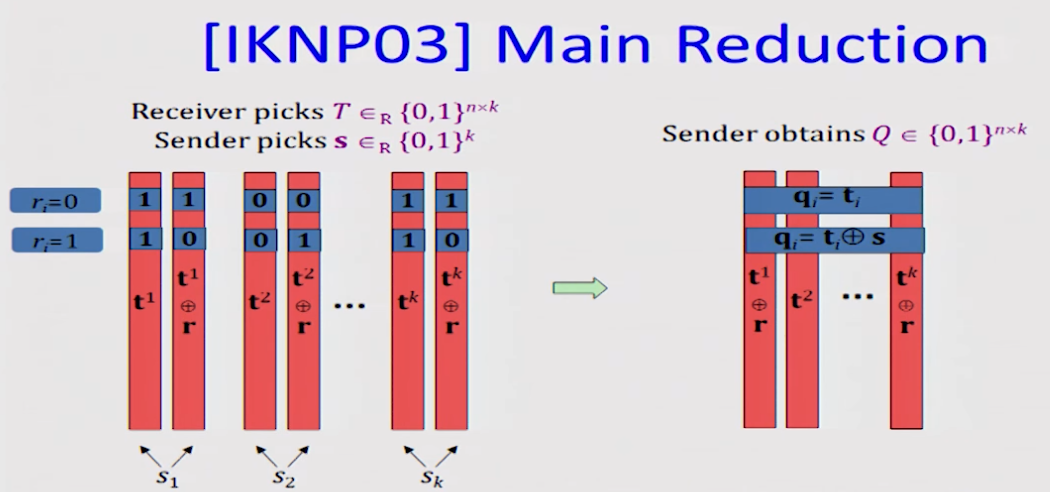(³より)を見れば分かりやすいが、 $r_i = 1$ ならばQのi行目の値が行列Tのi行目 $T_i$ の値そのままとなるか、もしくは $T_i$ の値を部分的に反転させたものになるかのどちらかであることから従う。部分的に反転させる条件とは結局の所 $s_j = 1$ となることであるから、 $Q_i$ は、 $T_i \oplus \mathbf{s}$ と一致する。
送信者が入手した行列Qの値をもとにして、送信者は受信者に対して以下の2n個の値を送る。ここで H(・)はハッシュ関数である。
1. $\mathbf{y} = \{ (y_{i, 0}, y_{i, 1}) \}_{i=1...n} = \{ (x_{i,0} \oplus H(Q_i), x_{i,1} \oplus H(Q_i \oplus \mathbf{s}) ) \}_{i=1...n}$
受信者は\mathbf{y}を受け取り、以下を出力する。この値は\{ x_{r_i} \}_{i = 1...n}と一致している。T_i = Q_iまたはT_i = Q_i \oplus \mathbf{s}であることに注意する。
1. $\mathbf{z} = \{y_{i, r_i} \oplus H(T_i) \}_{i=1...n}$

内部で紛失通信プロトコルを置き換える

上記のプロトコル内において、送信者がsを使って列を選択している過程は、n組の紛失通信プロトコルが、k組の別の紛失通信プロトコル（具体的なプロトコルがどのようなものかは気にしなくてもよい）によって置き換えられている過程であることに注意する。すなわち、長さnビットの2つの値を持つタプルがk組用意され、それぞれのタプルからいずれかの要素を選択している。

すなわち、IKNPプロトコル自体は拡張紛失通信プロトコルなのだが、その内部では送信者と受信者の役割を逆転させた別の紛失通信プロトコルがインスタンス数を変えて実行されているのである。

通信量について

上記(4)ではxのサイズをLビットとすると2nLビットの通信が発生している。

また上記(1)の内部紛失通信プロトコルではnビットのサイズの値を2k個通信している。このように大きなサイズの値をそのまま内部紛失通信プロトコルに与えると計算量上の効率が悪いため、送信値をシード値から生成される長い乱数によってマスクしてから通信することが考えられる。これを以下で解説する。

送信値の圧縮に必要な通信量

上記紛失通信プロトコル内で利用される値を圧縮するためには2nkビットの追加の通信が必要であることを以下で示す。

紛失通信の並列実行数を増やすのではなく、1つの紛失通信内でやりとりされる値の長さを圧縮・伸長する場合、アルゴリズムは単純である。紛失通信においてやりとりされる値を擬似乱数生成器を通すことで長いワンタイムパッドを作り、本来の値をマスクできるからである。
すなわち、疑似乱数生成器に通すためのシード値の長さをa(<< n)ビットとし、実際に選択したい値の長さをnビットすると、2k×aビット分の通信によってシード候補が送信され、さらにそのシードによってマスクされた値が直接 2k×nビット分送信されることになる。
結果として、 2ka + 2kn = 2k(a + n)≒2nkビット分の通信だけ行えば送信値を圧縮することができる。

通信量を犠牲にした紛失通信プロトコルインスタンス数の削減

すなわち、n組の紛失通信プロトコルは、追加で以下の通信量を犠牲にすることによって、k組の紛失通信プロトコルに効率的に置き換えることができると言える。

n組からk組のプロトコルへの変換: 2nLビット
nビットの値をk組のプロトコルで扱うために、値を圧縮する変換: 2nkビット

これは紛失通信プロトコルの1インスタンスあたりの実行にコストがかかり、紛失通信プロトコルに直接大きな値を入力することで計算コストが上がってしまう場合を想定している。

また、この削減は基本的にn >> kであるときに有用であるが、kはセキュリティパラメータでもあるため、一定以上小さくすることはセキュリティ要件上不可能である。
例えばk = 1とすれば行列Qの各行が取りうる値は2つしかないことになり、送信する値 $\mathbf{y}$ をランダムにマスクすることができなくなってしまう。