ランポート署名を改良した耐量子署名アルゴリズムSPHINCSの紹介

はじめに

この記事では¹の論文を解説します。SPHINCSはランポート署名²を実用的に使えるようにした規格です。ハッシュ関数にのみ依存し、公開鍵と秘密鍵のサイズを小さく抑えることができます。

解説

用語と記法

SPHINCSはパラメータを取ることで署名を作成できるアルゴリズムの総称であり、安全とみなされるパラメータを実際のパラメータとして定義した個別のアルゴリズム規格は SPHINCS-256 のようにインスタンスごとの個別の名前で呼ばれる。この解説の中では、基本的にはSPHINCS-256を扱う。以下n=256のように具体的な数字が入っているのはSPHINCS-256の値である。

メインのセキュリティパラメータを n = 256 とする。
F: \{0,1\}^n \rightarrow \{0,1\}^nをサイズnからnに移すハッシュ関数とする。
H: \{0,1\}^{2n} \rightarrow \{0,1\}^nをサイズ2nからnに移すハッシュ関数とする。
\mathcal{H}: \{0,1\}^n \times \{0,1\}^* \rightarrow \{0,1\}^m , m = \text{poly}(n)を、任意入力長のランダム化ハッシュ関数とする。
G_{\lambda}: \{0,1\}^n \rightarrow \{0,1\}^{\lambda n}をパラメータλを取る疑似乱数生成関数の族とする。
\mathcal{F}_\lambda: \{0,1\}^\lambda \times \{0,1\}^n \rightarrow \{0,1\}^{n}をパラメータλを取る疑似乱数関数の族とする。
\mathcal{F}: \{0,1\}^* \times \{0,1\}^n \rightarrow \{0,1\}^{2n}を任意の長さの入力を取る疑似乱数関数とする。

これらの関数はすべて同一のハッシュ関数から構築できるが、役割の都合上別のものとして記述している。

SPHINCSアルゴリズムで使われるハイパーツリー(hyper-tree)の高さをh = 60とする。
ハイパーツリーはd=12階層の層からなり、それぞれの層の高さはh/dである。

ヴィンターニッツ ワンタイム署名における時間空間計算量のトレードオフを決めるパラメータw = 16とする。少数回署名(few-time signature)アルゴリズムであるHORSTのパラメータ として k, t = 2^\tau, k\tau = mを満たすk,tがあるが、これは k = 32, t = 2^{16}とする。

ビット文字列xに対してx[i, j]はi番目のビットから始まるjビット分の部分ビット文字列を指すものとする。

ヴィンターニッツ ワンタイム署名 (Winternitz one-time signature; WOTS+)

ヴィンターニッツ ワンタイム署名（WOTS+）とは、ランポート署名のように一つの公開鍵に対して一度だけ署名できる署名方式（ワンタイム署名）であり、署名サイズと署名の計算時間の間にトレードオフがある。このトレードオフを規定するパラメータがwである。

n, wから以下のパラメータを定める。

l_1 = \lceil \frac{n}{\text{log}(w) } \rceil,\ l_2 = \lfloor \frac{ \text{log}(l_1(w-1)) }{ \text{log}(w) } \rfloor + 1,\ l = l_1 + l_2

SPHINCS-256の場合 l = 67となる。WOTS+では関数Fをつなげて以下のような連鎖関数cを作る。

入力x \in \{0,1\}^nとカウンターi、ビットマスク \bold{r} = (r_1, ..., r_j) \in \{0,1\}^{n\times j}、j\ge iとなるjに対して、 連鎖関数c^i(x, \bold{r}) = F(c^{i-1}(x, \bold{r}) \oplus r_{i})と定義する。i=0のとき、c^0(x, \bold{r}) = xである。

すなわち、この関数はラウンドiにおいて一つ前の値c^{i-1}(x,\bold{r})とビットマスク r_iのビットごとXORを取り、その結果をハッシュ関数Fに通している。
ここで \bold{r}_{a,b}を\bold{r}の部分文字列(r_a, ..., r_b)として定義する。b \lt aの場合は空文字列とする。

以下、WOTS+の本体の3つのアルゴリズムを説明する。

鍵生成アルゴリズムkg

入力シード\mathcal{S} \in \{0,1\}^nとビットマスク\bold{r} \in \{0,1\}^{n\times(w-1)}を受取り、秘密鍵skと公開鍵pkを返す。

まず\text{sk} = (\text{sk}_1, ..., \text{sk}_l) \leftarrow G_l(\mathcal{S})を生成する。つまり、長さnのシードを、l個の長さnの秘密鍵の値に拡張する。公開鍵は、\text{pk} = (\text{pk}_1, ..., \text{pk}_l) = (c^{w-1}(\text{sk}_1, \bold{r}), ..., c^{w-1}(\text{sk}_l, \bold{r}))として計算する。\mathcal{S}は秘密鍵skや公開鍵pkよりもサイズが小さく、skやpkは必要なタイミングで計算すればいいということに注意する。

署名アルゴリズムsign

nビットメッセージM、シード \mathcal{S}、ビットマスク\bold{r}を入力とし、署名値σを出力する。

まず、Mを整数値とみなしてw進数表現に変換する。M = (M_1, ..., M_{l_1}), M_i \in \{0,...,w-1\}とする。
次にチェックサムCを同様に計算し、w進数表現にする。(C_1, ..., C_{l_2}) = C = \sum_{i=1}^{l_1}(w - 1 - M_i)ここでCの値は、各項の値からC \le l_1 (w-1) のように上限が存在し、l_2の定義(上記の2進数logによる定義を参照)からCのw進数表現の長さは最大l_2となる。
次に B = (B_1, ..., B_l) = M || CをM,Cを結合させたl要素のw進数表現として定義する。内部秘密鍵 \text{sk}を鍵生成時と同様に G_l(\mathcal{S})によって生成する。署名は \sigma = (\sigma_1, ..., \sigma_l ) = (c^{b_1}(\text{sk}_1, \bold{r}), ..., c^{b_l} (\text{sk}_l, \bold{r}))となる。

すなわち、連鎖関数cが何回適用されるかはメッセージによって決まる。

検証アルゴリズムvf

メッセージM、 署名σ、ビットマスク\bold{r}を入力とし、pk'の値を返す。本来はtrue(成功)かfalse(失敗)を出力する必要があるが、これはSPHINCSにおいては全体の検証アルゴリズムの方で行われるため、WOTS+では行わない。
検証者は上記同様b_iを用意し、次の値pk'を計算する。
\text{pk}' = (\text{pk}_1', ..., \text{pk}_l') = (c^{w - 1- b_1}(\sigma_1, \bold{r}_{b_1 + 1, w-1 }), ..., c^{w - 1 - b_l} (\sigma_l, \bold{r}_{b_l + 1, w-1 } ) )

このpk'の値がpkと一致すれば成功、一致しなければ検証失敗となる。
公開鍵の値w-1に足りない回数だけ連鎖関数cを追加で実行している。秘密鍵を知らない攻撃者は、1~w-1の任意ラウンド回数ハッシュ関数を逆算する必要がある。w=1の場合はほとんどランポート署名と変わらない。
wの値を増やすと署名の長さは短くなる代わりに、計算量が増える。

バイナリハッシュ木 / L木

SPHINCSにおけるバイナリハッシュ木は以下のような図の木になる（間にビットマスクQが挟まっていること以外は普通のマークルツリーと同じ）。

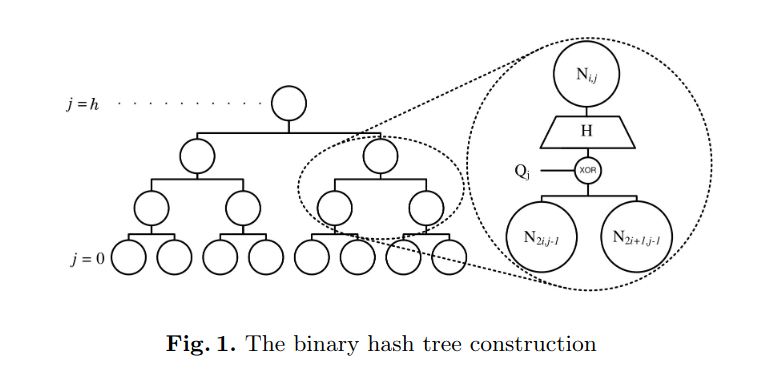
バイナリハッシュ木は高さhで常に2^hの葉ノードを持ち、それらの葉はnビットの値L_i, i \in [2^h - 1]を持つ。中間のそれぞれのノードN_{i,j}は0\lt j\le h, 0 \le i \lt 2^{h-j} (iが横の番号、jが高さの番号)に対してnビットの値を持っている。
木を構築するには、hビットのビットマスク\bold{Q}_j \in \{0,1\}^{2n}, 0 \lt j \le hが使われる。葉ノードに対しては N_{i,0} = L_iと定義する。内部ノード N_{i,j}の値は N_{i,j} = H((N_{2i, j-1} || N_{2i+1, j-1}) \oplus \bold{Q}_j )として計算される。ルート(根)に当たる部分の値\text{ROOT}=N_{0,h}とする。

また、重要な概念として葉L_iに対する認証パス\text{Auth}_i = (A_0, ..., A_{h-1})があり、下図に示されている。

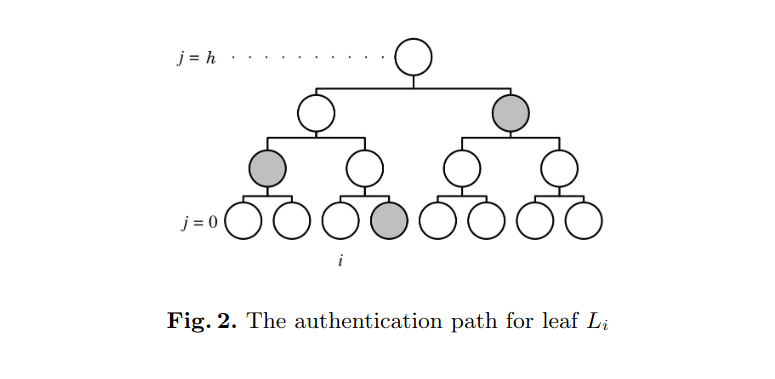
葉L_iと対応する認証パス\text{Auth}_iから以下のアルゴリズムでROOTの値を計算することができる。

アルゴリズム1（マークルツリーの整合性チェックアルゴリズムと同じ）

入力: 葉のインデックスi、葉L_i、L_iの認証パス\text{Auth}_i = (A_0, ..., A_{h-1})
出力: 葉L_iを含む木のROOTの値

P_0 \leftarrow L_iをセットする。
j = 1,...,hに対して
　\lfloor i/2^{j-1}\rfloor = 0\ \text{mod}\ 2ならば P_j \leftarrow H((P_{j-1} || A_{j-1}) \oplus \bold{Q}_j)
　\lfloor i/2^{j-1}\rfloor = 1\ \text{mod}\ 2ならば P_j \leftarrow H((A_{j-1} || P_{j-1}) \oplus \bold{Q}_j)
　を代入
最後にP_hを返して終了。

L木

L木は上記で説明したバイナリハッシュ木に小さな変更を加えたものである。バイナリハッシュ木の葉は2のべき乗になっている数の葉しか扱えないが、L木においては2のべき乗でない数lも葉の数として使える。L木はバイナリハッシュ木の「右ノードが不在の左ノード」の階層を上昇させ、「他のノードの右側子ノード」になる場所で止めるようなものになる。これはWOTS+の公開鍵の要素を保存しておくのに使われる。L木の高さは\lceil \text{log}(l)\rceilになり、ビットマスクも\lceil \text{log}(l)\rceilだけ必要になる。

HORST

HORSTは長さmのメッセージに対する署名でk\tau = mを満たす値k, t = 2^\tauを用いる。HORSTはHORSの改良版でバイナリハッシュ木を使って公開鍵のサイズをtnビットからnビットに減らし（※ビットマスクを使いまわすことで、サイズを0とした場合。もしビットマスクを使い回さない場合、公開鍵サイズは(2\tau+1)n \lt tnとなる）、署名と公開鍵を結合させた文字列のサイズをtnビットから(k(\tau - x + 1) + 2^x)nビットに減らすことになった。xはt,kに応じて決まる値で、k(\tau - x + 1) + 2^xが最小になるように決める。SPHINCS-256においてはx = 6である。

WOTS+とは違い、HORSTは複数回同じ鍵で署名ができる。しかし、署名をするたびにセキュリティが低下していく。

鍵生成アルゴリズムkg

シード\mathcal{S} \in \{0,1\}^n, ビットマスクQ \in \{0,1\}^{2n \times \text{log} (t)}を入力として、公開鍵\text{pk}を出力する。
まず内部秘密鍵 \text{sk} = (\text{sk}_1, ..., \text{sk}_t) \leftarrow G_t(\mathcal{S}) を計算する。i \in [t-1]に対して葉ノードはL_i = F(\text{sk}_i)として計算され、高さ\text{log}(t)のバイナリハッシュ木がビットマスクQを使って計算される。

署名アルゴリズムsign

メッセージM \in \{0,1\}^m、 シード\mathcal{S} \in \{0,1\}^n、ビットマスクQ \in \{0,1\}^{2n \times \text{log} (t)}を入力として、署名値 (\sigma, \text{pk})を出力する。

まず内部秘密鍵skがアルゴリズムkg同様に計算される。次にMを長さlog(t)ビットずつ最大kブロックに分割し、それぞれのブロックを最大 log(t) ビットの符号なし整数とみなす。つまりM = (M_0, ..., M_{k-1})となる。
署名値σ は \sigma = (\sigma_0, ..., \sigma_{k-1}, \sigma_{k} )と表され、\sigma_0から\sigma_{k-1}は\sigma_i = (\text{sk}_{M_i}, \text{Auth}_{M_i}), i \in [k-1]になる。
これは M_i番目の秘密鍵と、木の下からの高さ\tau - x（=上からの深さx）までの認証パス (A_0, ..., A_{\tau -1 - x})を含む。（※これだけでは葉から根までの完全な認証パスの検証は行えない）

また、最後の署名要素である\sigma_kに関してはバイナリハッシュ木の高さ\tau - xにおける全2^x要素、すなわち (N_{0,\tau-x}, ..., N_{2^x - 1,\tau-x})が入る。

この署名値σに加えて、アルゴリズムは公開鍵pkを出力する。

検証アルゴリズムvf

メッセージM \in \{0,1\}^m、 署名値σ、ビットマスクQ \in \{0,1\}^{2n \times \text{log} (t)}を入力として値pk'を出力する。
まずアルゴリズムsignと同様に、各M_iを計算する。次に各i \in [k-1]に対してy_i = \lfloor M_i / 2^\tau -x\rfloorとして、インデックスM_iに対してアルゴリズム1を適用する。

アルゴリズム1の入力は L_{M_i} = F(\sigma_i^1), \text{Auth}_{M_i} = \sigma_i^2である。\sigma_i^1, \sigma_i^2はそれぞれの署名配列のi番目の値における第一項、第二項である。

アルゴリズム1の出力は N'_{y_i, \tau - x}となる。
その後、すべてのi \in [k-1]に対してアルゴリズム1の出力であるN'_{y_i, \tau - x}と、\sigma_kの中身であるN_{y_i, \tau - x}が一致するかどうかを確認する。もし一致するならば、\sigma_kの値から\text{ROOT}を計算し、その値を返す。一致しなければ、\text{fail}を返す。

理論上のパフォーマンス

以下ではビットマスクの計算領域については(共通化出来るため)省略している。
また以下では疑似乱数生成の回数とハッシュ関数の実行の回数を、ハッシュ関数の区別は行わずに記載する。

サイズ

HORSTの秘密鍵はnビットシード値で表現される。公開鍵は単一のnビットハッシュになる。署名値はk個の内部秘密鍵要素と、k個の「log(t)-xの長さを持つ認証パス」を持つ。これに加えて最後の要素である \sigma_kは2^x個のノード(サイズnビット)を持ち、合計サイズは(k(\text{log}(t) -x +1) + 2^x) nビットになる。

実行速度

鍵生成は1回のG_tの実行と、葉ノードを生成するためのt回のハッシュ計算、公開鍵を生成するためのt-1回のハッシュ計算が必要になり、合計のハッシュ計算回数は 2t-1回になる。

署名実行時にはROOTの計算が必要になるため鍵生成と同じ回数のハッシュ計算回数(2t-1)が必要になる。

署名検証時には、葉ノードの値を計算するためにk回のハッシュ計算が必要になる。また、高さlog(t)-xにおけるノードを計算するためにはk要素に対してそれぞれ log(t)-x回のハッシュ計算が必要になる。さらに、\sigma_kからROOTの値を計算するためには2^x - 1回のハッシュ計算が必要になる。よって合計 k(\text{log}(t) - x + 1) + 2^x -1回のハッシュ計算が必要になる。

まとめ

まとめると、このHORSTというスキームでは署名対象のメッセージをランダム化して、バイナリハッシュ木の葉をランダムにいくつか選ぶように対応させる。
そのランダムに選んだ葉と一致するように元のハッシュ原像を公開する。当然、一番最初に作成し公開した署名の場合はどのハッシュ原像も公開されていなかったものであるため、ランポート署名と同程度のセキュリティである。2回目以降の署名では、すでに公開されたハッシュ原像と一致していないものが含まれれば、安全である。
何回も署名を繰り返すことによって、「まだ公開されていない原像をランダムに選択できる確率」は低くなっていく。そのうち、攻撃者が何らかのメッセージに対して「すでに公開された原像のみから構成できる署名値」を発見してしまった場合、攻撃者は署名の偽造が可能になる。

例えば、以下の図のように初回のメッセージMが赤文字で記された原像を選択し、2回目のメッセージM'が青文字で記された原像を選択したとする。M'_1はM_1と同じ原像を選択してしまっているが、M'_0, M'_2はこれまで公開されていなかった原像を選択しているので、2回目のメッセージM'に対して有効な署名が作れている。

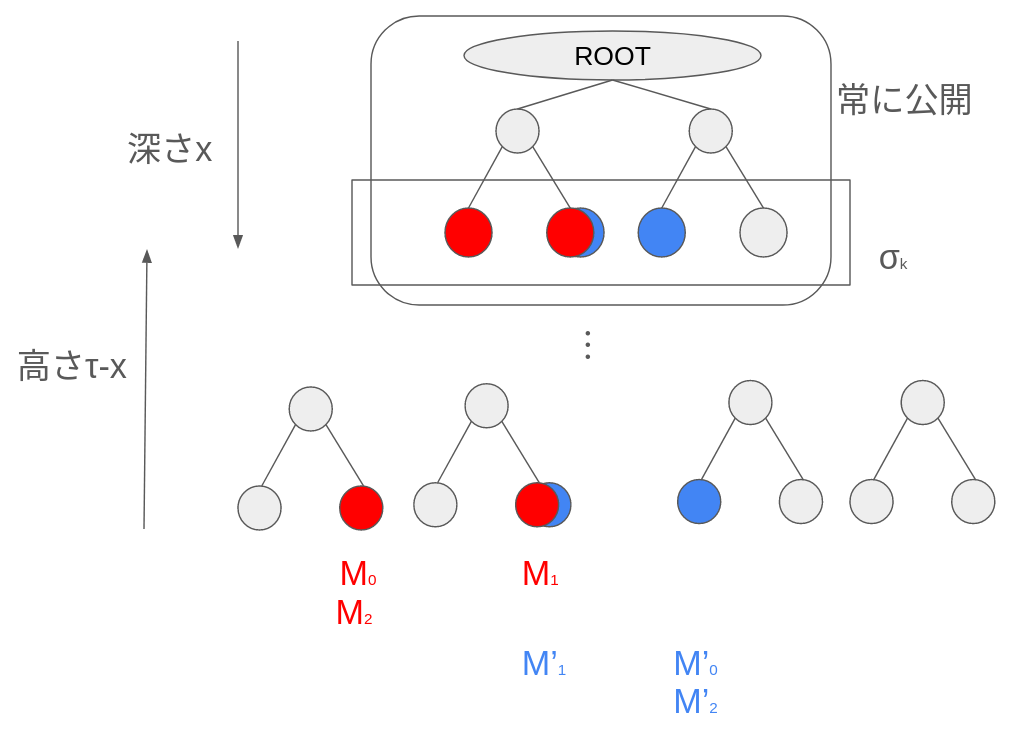
SPHINCS

上記のHORST, WOTS+, L木などを用いて、SPHINCSのアルゴリズムを定義する。
SPHINCSの鍵ペアは、SPHINCSアルゴリズム自体の「仮想的な」構造の表現にもなっている。
SPHINCSは高さh/dの木がd層重なってできた、高さhのハイパーツリーからなる。
それぞれの木は以下のようになっている。

それぞれの木における 2^{h/d}個の葉ノードは 2^{h/d}個のL木のルートノードであり、それぞれのL木のルートノードはWOTS+鍵ペアを圧縮した表現と見なす。
すなわち、それぞれの木は 2^{h/d}個のメッセージに署名できる鍵ペアであり、ハイパーツリーはそれがd個重なったものと見ることができる。

d-1層（上から1つ目の層）においては、ハイパーツリーは1つだけ木を持つ。d-2層（上から2つ目の層）においては、ハイパーツリーは2^{h/d}個の木を持つ。d-2層の木のルートノードは、d-1層の木のWOTS+署名によって署名されている。

一般に、i層は2^{(d-1-i) h/d}個の木から構成されており、これらの木のルートノードはi+1層のWOTS+鍵ペアによって署名されていることになる。

最後に、第0層においては、それぞれのWOTS+署名鍵ペアは、HORST公開鍵を署名するために使われる。

最初に「仮想的な」構造と表現したのは、シード値とビットマスクを選択することによって構造の全ての値が決まり、全体の構造が計算されることはないからである。
シード値は秘密鍵の一部であり、疑似乱数による鍵生成に使われる。

理解のため、SPHINCSの署名を表現した以下の図を見よ。すなわち、SPHINCSの署名はこのハイパーツリーの中の一つのパスとして表現される。

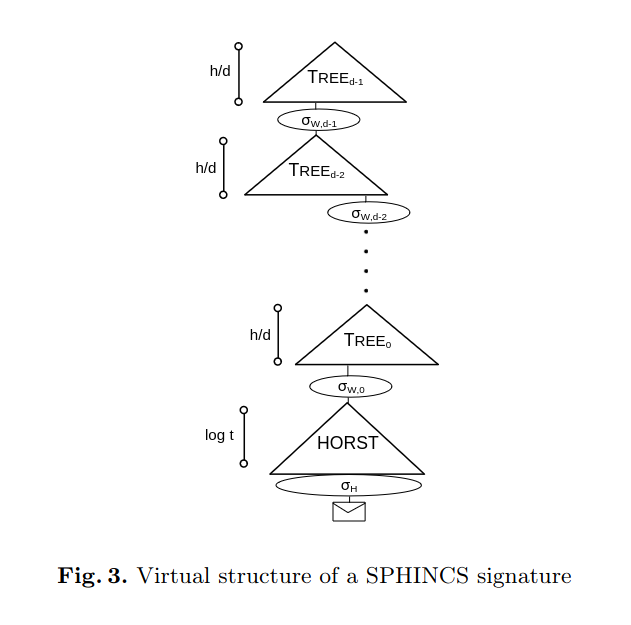
このパスはd個の木\text{TREE}_i, i\in [d-1]からなり、それぞれのバイナリハッシュ木は2^{h/d}個のL木のルートノードを認証し、それぞれのL木はWOTS+鍵ペアの公開鍵を葉ノードとして持っている。
それぞれの木は1階層下にある木をWOTS+署名\sigma_{W,i}を認証している。例外は最下層の木 \text{TREE}_0で、これはWOTS+の署名によってHORSTの公開鍵を認証している。

最後に、HORSTの鍵ペアが実際のメッセージを署名するのに使われる。ハイパーツリー内においてどの木が使われるのか（したがって署名においてどのWOTS+署名値を使うか）は、この図には記載されていないが、疑似乱数によって選択されたインデックスによって決定される。

ここで、疑似乱数による鍵生成のために簡単なアドレススキーム（番地を決定するスキーム）を決めておく。アドレスとは長さ a = \lceil \text{log}(d+1) \rceil + (d-1)h/d + h/d = \lceil \text{log}(d+1) \rceil + hの ビット列である。

WOTS+鍵ペアのアドレスを得るには、まず木が所属している層の番号をlog(d+1)ビットの文字列としてエンコードする。（最上位の1つだけ木がある層はd-1層とする。）
さらに、層内部の木の番号を(d-1)(h/d)ビットの文字列としてエンコードし、先の層の番号の文字列の末尾に追加する。（ここで層内部の木の番号は左から数えて0から始まり、最も右の木まで数える）
最後に、木内部のWOTS+鍵ペアのインデックスを(h/d)ビットの文字列としてエンコードし、上記の文字列の末尾に追加する。（ここでもWOTS+鍵ペアは左から数えて0から始まり、最も右の木まで数える）

HORST鍵ペアのアドレスは、HORST鍵ペアを署名するのに使ったWOTS+鍵ペアのアドレスから作成するが、先頭の「木が所属している層の番号をlog(d+1)ビットの文字列としてエンコードする」部分で、番号をdとして固定してエンコードする。

SPHINCS-256においては、このアドレスは64ビットになる。

鍵生成アルゴリズム

鍵生成アルゴリズムはまず(\text{SK}_1, \text{SK}_2) \in \{0,1\}^n \times \{0,1\}^nの2つの値を生成する。\text{SK}_1は疑似乱数鍵生成に使われる。\text{SK}_2は署名時に、予期できないインデックスを生成するのと、署名対象のメッセージをハッシュ化する際に、値をランダム化するのに使われる。

また、p = \text{max}\{w-1, 2(h + \lceil \text{log}(l) \rceil), 2\text{log}(t)\}個のnビット一様ランダム値を Q \leftarrow \{0,1\}^{p\times n}がビットマスクとして生成される。これらのビットマスクはWOTS+、HORST、各種のバイナリハッシュ木に使われる。以下において、Q_{\text{WOTS+}}をQのうち最初のw-1個の、長さnのビットマスクとして定義する。同様にQ_{\text{HORST}}をQのうち最初の2\text{log}(t)個のビットマスクとして定義し、Q_{\text{L-Tree}}をQのうち最初の2\lceil \text{log}(l) \rceil個のビットマスクとして定義し、Q_{\text{Tree}}をQのうち最初の2h個のビットマスクとして定義する。

鍵生成アルゴリズムの残りの部分は、d-1層におけるルートノードを生成することだけになる。d-1層における単一の木の葉ノードにあたるWOTS+鍵ペアが複数生成される。

アドレスA = (d-1 || 0 || i), i \in [2^{h/d} - 1]における鍵ペアのシードは \mathcal{S}_A \leftarrow \mathcal{F}_a (A, \text{SK}_1)として、疑似乱数生成関数にAと\text{SK}_1 を与えることで生成する。

一般に、アドレスAに対する鍵ペアのシードは \mathcal{S}_A \leftarrow \mathcal{F}_a (A, \text{SK}_1)とし、\text{SK}_1を知っているならば、この鍵ペアシードの生成アルゴリズムにもアクセスできるものとする。WOTS+公開鍵は\text{pk}_A \leftarrow \text{WOTS.kg}(\mathcal{S}_A, Q_{\text{WOTS}+})で生成する。

木のi番目の葉ノードであるL_iはビットマスクQ_{\text{L-Tree}}を使って\text{pk}_Aを（l要素lnビットから1要素nビットへと）圧縮したL木のルートノードになる（下図参照）。

以下の図は https://www.mdpi.com/2076-3417/11/5/2082 から。

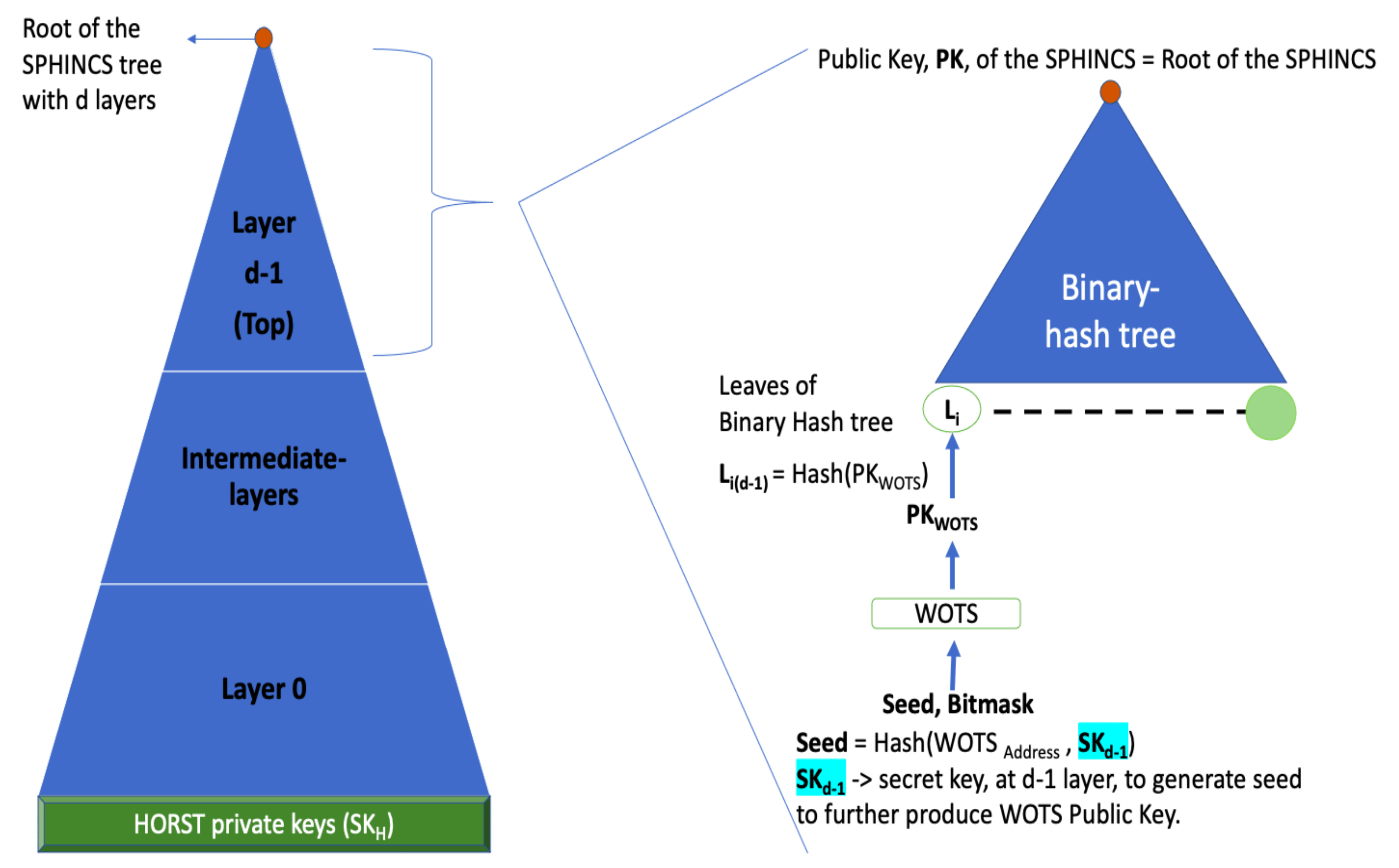
最後に、葉ノードL_iからバイナリハッシュ木を生成し、そのルートノードを\text{PK}_1とする。SPHINCSの秘密鍵と公開鍵は ((\text{SK}_1, \text{SK}_2, Q), (\text{PK}_1, Q))であり鍵生成アルゴリズムはこの鍵ペアを返す。

署名アルゴリズム

メッセージM \in \{0,1\}^{*}と秘密鍵\text{SK} = (\text{SK}_1, \text{SK}_2, Q)を入力として、署名値 \Sigmaを返す。

まず、メッセージと秘密鍵に対してランダム化メッセージダイジェストD \in \{0,1\}^{m}を計算する。
最初に疑似乱数R = (R_1, R_2) \in ( \{0,1\}^{n} \times \{0,1\}^{n})がR \leftarrow \mathcal{F}(M, \text{SK}_2)として計算される。次にD \leftarrow \mathcal{H}(R_1, M)がRの最初のnビットをランダムネスとして使ってメッセージMのランダム化ハッシュとして計算される。Rの後半nビットはHORSTの鍵ペアを選択するのに使われる。すなわち、R_2の最初のhビットがhビットインデックスi \leftarrow \text{CHOP}(R_2, h)として計算される。

署名は決定的アルゴリズムであり、全ての「ランダムネス」は疑似乱数生成関数\mathcal{F}によって生成されるため真のランダムネスは必要としていないことに注意せよ。

インデックスiが与えられた上で、アドレスA_{\text{HORST}} = (d || i[0, (d-1)h/d] || i [(d-1)h/d, h/d]) によって指定されるHORST鍵ペアがメッセージダイジェストDを署名するのに選択される。すなわち、インデックスiのうち、0ビット目から(d-1)h/dビット目までがd番目の層においてどの木を選択するかに使われ、残りの(d-1)h/d + 1ビット目からh/dビット目までが木の中においてどの葉ノードを選択するかに使われる。
HORSTの署名と公開鍵 (\sigma_H, \text{pk}_H) \leftarrow (D, \mathcal{S}_{A_\text{HORST}}, Q_{\text{HORST}})は、HORSTのビットマスクと \mathcal{S}_{A_\text{HORST}} \leftarrow \mathcal{F}_a(A_\text{HORST}, \text{SK}_1)を用いて計算される。

SPHINCS署名\Sigma = (i, R_1, \sigma_H, \sigma_{W,0}, \text{Auth}_{A_0}, ..., \sigma_{W,d-1}, \text{Auth}_{A_{d-1}} )は、インデックスiの他にはランダムネスR_1、HORST署名\sigma_H、ハイパーツリーの層一つにつきWOTS+署名と認証パスのペア (\sigma_{W, i}, \text{Auth}_{A_i}), i \in [d-2]を含む。

これらのWOTS+署名は以下のように計算できる。
アドレスA_0に対応するWOTS+鍵ペアは\text{pk}_Hを署名するのに使われる。ここで A_0はA_{\text{HORST}}の最初の\lceil \text{log}(d+1)\rceilビットを0に置き換えたものである。

HORST公開鍵\text{pk}_Hに対してWOTS+のビットマスクを使いWOTS+で署名すると、\sigma_{W,1} \leftarrow (\text{pk}_H, \mathcal{S}_{A_0}, Q_{\text{WOTS+}})のような署名値を入手できる。そして、署名に使ったWOTS+鍵ペアの公開鍵に対する認証パス（最下層のバイナリハッシュ木の内部における認証パス）\text{Auth}_{i[(d-1)h/d, h/d]}が計算できる。次に、WOTS+公開鍵\text{pk}_{W, 0} \leftarrow \text{WOTS.vf}(\text{pk}_H, \sigma_{W,0}, Q_\text{WOTS+})を計算する。

\text{pk}_{W, 0}をL木を使って圧縮してnビットの葉ノードの値としてセットした後、アルゴリズム1を適用することによって、「L木のルートノード」（＝バイナリハッシュ木の葉ノード）と「最下層のバイナリハッシュ木の内部における認証パス」と、「WOTS+鍵ペアを選択したインデックス」から「最下層のバイナリハッシュ木のルートノード」\text{ROOT}_0が計算される。

このプロセスがレイヤー1からd-1まで繰り返されるが、以下の2点のみ違いがある。
(1) まずj層1 \le j \lt dにおいてWOTS+は 前のステップで生成された\text{ROOT}_{j-1}を署名するのに使われる。
(2)またj層におけるWOTS+鍵ペアのアドレスは A_j = (j || i[0, (d-1-j)h/d] || i[(d-1-j)h/d, h/d])として計算される。
すなわち、それぞれの層において、「木を指定している部分のアドレス」の最後のh/dビットの部分が新しく「葉ノードを指定するアドレス」に加わり、「もともと（前の層において）木を指定していたアドレスのうちの、最後のh/dビットの部分を除いた残りの部分」が新しく「木を指定している部分のアドレス」になる。

これは、層を上がるにつれて層の中に含まれる木の数は (h/d) 分の 1に減っていくことが理由である（ただし、同じインデックスiを部分的に使いまわすことによって、層ごとに指定する木のインデックスが偏ってしまうリスクがあるのではないか？）。

最終的にこの署名アルゴリズムは\Sigma = (i, R_1, \sigma_H, \sigma_{W,0}, \text{Auth}_{A_0}, ..., \sigma_{W,d-1}, \text{Auth}_{A_{d-1}} )を返却する。

検証アルゴリズム

メッセージM \in \{0,1\}^*、署名値\Sigma、公開鍵\text{PK}を入力として、検証成功の場合trueを、失敗の場合falseを返す。
まずメッセージダイジェスト D \leftarrow \mathcal{H}(R_1, M)を署名に含まれるランダムネスR_1を使って計算する。\text{PK}に含まれるビットマスクQ_{\text{HORST}}とHORST署名からHORST公開鍵\text{pk}_H \leftarrow \text{HORST.vf}(D, \sigma_H, Q_{\text{HORST}})を計算する。もしHORST.vfがfailを返すならば、検証アルゴリズムもfalseを返す。

WOTS+ビットマスクとWOTS+署名とHORST.vfに返された公開鍵\text{pk}_HからWOTS+公開鍵\text{pk}_{W,0} \leftarrow \text{WOTS.vf}(\text{pk}_H, \sigma_{W,0}, Q_\text{WOTS+})を計算する。\text{pk}_{W,0}に対応する葉ノードL_{i[(d-1)h/d, h/d]}を計算するためにL木が使われる。その後アルゴリズム1によって、インデックス i[(d-1)h/d, h/d]と、葉ノードL_{i[(d-1)h/d, h/d]}と、認証パス\text{Auth}_0によって最下層の木のルートノード\text{ROOT}_0を計算する。

その後、このプロセスが第1層からd-1層まで繰り返されるが、以下の2点の違いがある。

(1) まず、層j 1\le j \lt dにおいてWOTS+公開鍵\text{pk}_{W,j}を計算するために、一つ前の層のルートノード\text{ROOT}_{j-1}が使われる。
(2) L木を使って\text{pk}_{W,j}から計算される葉ノードはL_{i[(d-1-j)h/d, h/d]}となる。すなわち、木の中における葉ノードのインデックスはiの後ろj(h/d)ビットを切り捨てたビット文字列のうち、末尾のh/dビット分を使用するものとする。

第d-1層におけるプロセスを実行した後、\text{ROOT}_{d-1}という値がトップの層の単一の木におけるルートノードとなる。この値が、公開鍵における第一項の値と比較される。すなわち、\text{PK}_1と\text{ROOT}_{d-1}が等しいかを確認する。
もし等しければ検証関数はtrueを返し、等しくなければfalseを返す。

理論上のパフォーマンス

以下では疑似乱数生成関数PRFと、疑似乱数生成器PRGとハッシュの理論的な実行回数を調べるが、異なるPRF, PRG, ハッシュを同一にカウントしている。

サイズ

SPHINCSの秘密鍵は2個のnビットシードとp = \text{max}\{w-1, 2(h+\lceil \text{log}(l) \rceil), 2 \text{log}(t) \}個からなるnビットのビットマスクからなり、合計では(2+p)nビットになる。公開鍵は単一のnビットハッシュとビットマスクを含むので、合計サイズは(1+p)nビットになる。署名は1つのhビットインデックスとnビットのランダムネスを含む。さらに、署名はHORST署名(k((\text{log}(t) - x + 1) + 2^x)nビット)と、d個のWOTS+署名（それぞれlnビット）と、h個の認証パスノード(それぞれnビット)を含んでいる。そのため、署名全体のサイズは((k(\text{log}(t) -x +1) + 2^x) + dl + h + 1)n + hビットになる。

実行速度

SPHINCSの鍵生成はハイパーツリーのトップの木を構築することで行われる。
葉ノードを生成するために以下の処理が2^{h/d}回行われる。

• 1回の疑似乱数生成関数実行
• 1回の疑似乱数生成器実行
• 1回のWOTS+鍵生成実行(lw個のハッシュ計算)
• L木の計算(l-1回のハッシュ計算)

木を構築するために、さらに 2^{h/d} - 1回のハッシュ計算が必要になる。
合計すると、2^{h/d}回の疑似乱数生成関数と疑似乱数生成器の実行、(l(w+1))2^{h/d} - 1回のハッシュ計算となる。

署名時には以下が必要である。

• インデックス、メッセージダイジェスト生成のための乱数、メッセージハッシュ計算のために、1回の疑似乱数生成関数実行
• さらにHORSTのシードを生成し、HORST署名を生成するために1回の疑似乱数生成関数実行
• 加えて、d個のバイナリハッシュ木を構築する必要があり、鍵生成時のd倍の回数の木構築の実行
• WOTS+署名はWOTS+鍵生成を実行する間に生成することができるため、追加のコストはかからない

合計すると、d 2^{h/d} + 2回の疑似乱数生成関数実行、d 2^{h/d} + 1回の疑似乱数生成器実行、2t + d((l(w+1)) 2^{h/d} -1)回のハッシュ計算となる。

最後に、署名検証には

• メッセージダイジェストのハッシュ
• 1回のHORST検証
• d回のWOTS+検証（最大lw回のハッシュ計算）
• L木の計算
• ルートノードを計算するためのh/d-1回のハッシュ計算

が必要であり、合計するとk((\text{log}(t)) - x + 1)+2^x + d(l(w+1) - 2) + h回のハッシュ計算が必要になる。

感想

SPHINCS-256の署名サイズ(41kB)がECDSA(64B)と比較すると1000倍近くあるのでそのままブロックチェーンに載せるのは厳しいと思うのですが、SPHINCSをベースにすると暗号学的仮定を最小限まで減らせるので、計算検証履歴を圧縮できるSTARKと併用することで、純粋なハッシュベースの暗号通貨を構築することは可能性としてありえるのではないかと思いました。
PoW、署名、ブロックチェーン圧縮の全要素が共通のハッシュ関数に依存する形で構成できるならば、より安全性の高いシステムに繋がると考えます。
なお改良版のSPHINCS+³という方式ではさらに署名サイズが小さくなっているようです。実用的には、既存の楕円曲線暗号方式（例えばEd25519）と組み合わせ、両方の署名検査をパスすることを要求するハイブリッド署名方式⁴がより安全なスキームとして提案されています。
ハッシュベース暗号なのにXMSS⁵と違いステートレスで扱える方法の発明は純粋に面白かったです。

※関連する脆弱性⁶についても興味があったら見てみてください。

参考文献