ハッシュベースの署名アルゴリズムSPHINCSを改良したSPHINCS+(C)の解説

はじめに

本記事ではハッシュ関数を使った署名アルゴリズムSPHINCSについて解説した前回のブログ記事¹に引き続き、SPHINCSの改良版である SPHINCS+²と SPHINCS+C³の簡単な解説を行います。いずれも前回の記事が前提になっているので、そちらを先に読んでみてください。

SPHINCSとSPHINCS+の相違点

SPHINCS+のアルゴリズムの相違点を解説したブログ⁴で、相違点が解説されています。
SPHINCS+では署名サイズがSPHINCSよりも小さくなっている他、セキュリティ上の不備が指摘されていた点を修正しています。

署名サイズを小さくするための改良としてHORSTの代わりにFORSという少数回署名(few-time signature)アルゴリズムが取り入れられており、これについて解説したstackexchangeの回答⁵をベースに以下で解説してみます。

FORS (Forest Of Random Subsets)

もともとSPHINCSではHORSTという少数回署名アルゴリズムを、ハイパーツリーの一番下の層に置いていました。SPHINCS+では、これをFORSというより署名サイズの小さい別の少数回署名アルゴリズムに置き換えています。

鍵生成

2^a個の要素を葉ノードとして持つような高さaのバイナリハッシュ木（マークル木）がk個あるとします。c(1\le c\le k)番目のバイナリハッシュ木のうち、左からd(1\le d \le 2^a )番目の要素をx_{c,d}とします。実際には、これらのマークル木にはx_{c,d}ではなく、H(x_{c,d})のようにハッシュ関数を通した値が入っているとします。

これらk個のマークル木のルートノードを計算し、k個のルートノードを結合させてハッシュ値を1回取ることで、公開鍵とします。秘密鍵は、各x_{c,d}の要素です。

以下画像は⁶から転載。l=a=3, N=kと読み替えてください。また、skはxに対応しています。

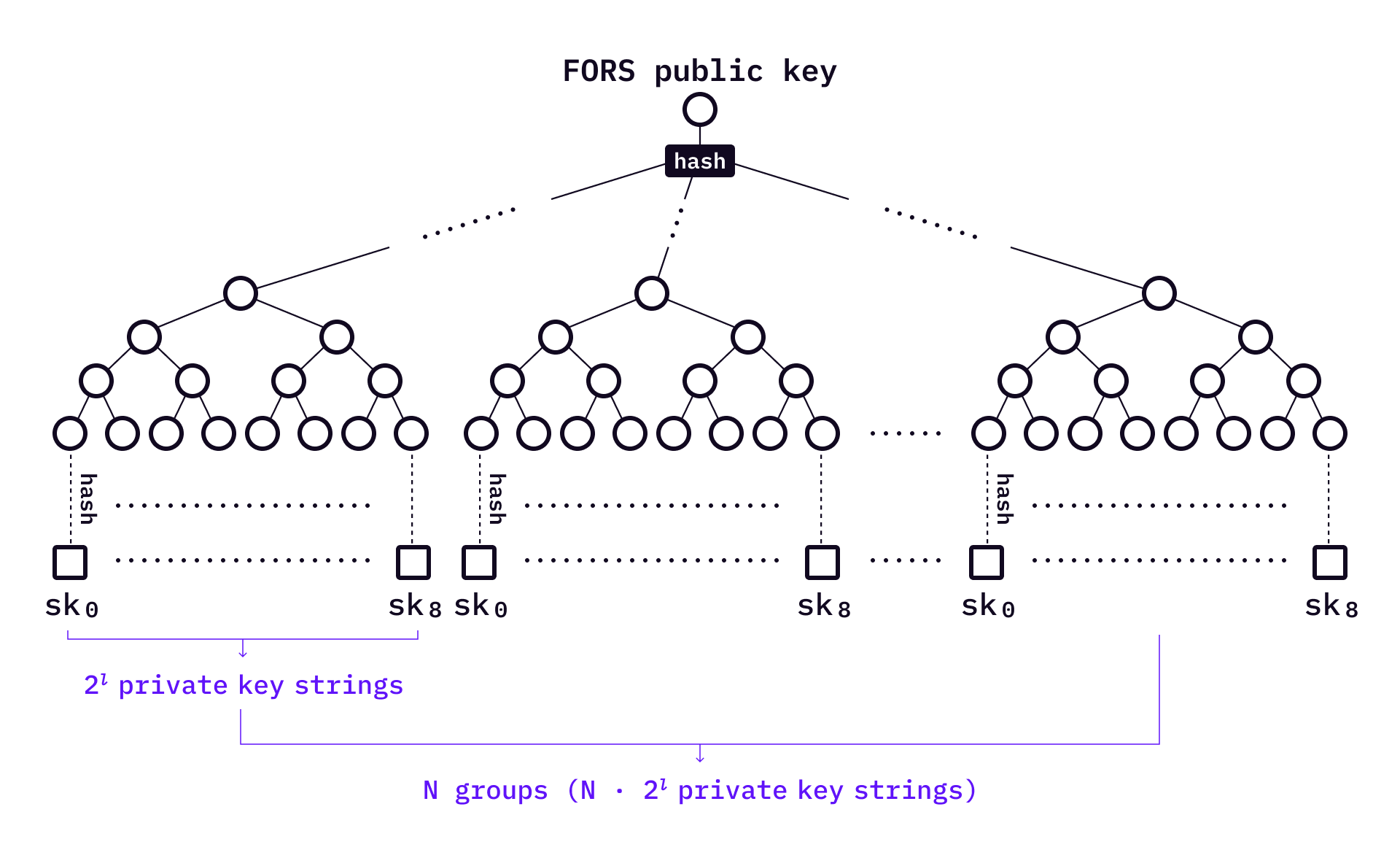
署名

メッセージmをaビットずつ区切ってk個の値 (m_1, ..., m_k) (0\le m_i \le 2^a)にします。このm_iを使って、(x_{1, m_1}, ..., x_{i, m_i}, ..., x_{k, m_k})のようなk個の秘密鍵を公開します。さらに、この秘密鍵はk個のマークル木から一つずつ取られているので、k個のマークル木のルートまでの認証パスも公開します。こうして公開された値が署名値になります。

検証

検証者は署名値のマークル木が正しく認証されることと、メッセージから計算したインデックスの番号の秘密鍵が公開されていることと、マークル木のルートノードを結合させてハッシュ値を取った値が公開鍵に一致していることを確認します。

有効な署名回数の見積もり

2^\lambda回署名した後で、攻撃者が署名を偽造できる確率は以下のとおりです。
全部で秘密鍵は 2^a k要素あり、そのうち最大2^\lambda k要素を公開しています。攻撃者が選んだメッセージに対して、メッセージのチャンクk個がすべて公開されている確率は ( \frac{2^\lambda k} { 2^a k} )^k = 2^{k(\lambda -a )}となります。例えばSPHINCS+-128sにおいては(a,k)=(12,14)であり、\lambda \le 12 - 128/14となる\lambdaに対して 2^\lambdaの最大整数値は7となるので、このパラメータでは7回まで128ビットのセキュリティで署名が偽造されずに作成できることになります。

SPHINCS+とSPHINCS+Cの相違点

youtubeの解説動画⁷をベースに解説します。

SPHINCS+CはSPHINCS+の署名サイズを、セキュリティを保ったまま圧縮させる改良アルゴリズムです。なおCは多分Compression(圧縮)だろうと勝手に思っています。

SPHINCS+の中ではWOTS+（ワンタイム署名アルゴリズム）とFORS（少数回署名アルゴリズム）というアルゴリズムが使われています。これらの計算時に、それぞれの署名サイズと署名時間を削減した WOTS+C, FORS+C というアルゴリズムを使うことで、SPHINCS+全体の署名サイズと署名時間を削減します。

具体的には、128ビットのセキュリティ条件下において SPHINCS+ では 7856 バイトだった署名値が SPHINCS+C では 6304 バイトになっています。

WOTS+C

WOTS+¹では内部でメッセージに加えてチェックサムを計算していましたが、このチェックサムを署名時に計算する代わりに、チェックサムが定数になるように、秘密のソルト値をブルートフォース計算しておくことでセキュリティを保ったまま署名のサイズを削減しています。

攻撃者が同様の条件の署名を偽造するためには、結局同じだけブルートフォース計算が必要になると考えられます。

FORS+C

FORSではk個のマークル木を使っていましたが、k個目の木のマークルルート値が定数になるように、秘密のソルト値をブルートフォース計算することでセキュリティを保ったまま署名のサイズを削減しています。

こちらもWOTS+と同様に、攻撃者が同様の条件の署名を偽造するためには、結局同じだけブルートフォース計算が必要になると考えられます。

感想

SPHINCSなどのハッシュベース署名はサイズを犠牲にしたセキュリティの高さが売りですが、署名サイズを削減する余地がまだ残っていたというのは興味深いです。ただ、ハイパーツリーを導入した際のように根本的なデータ構造を変えるものではなく、ブルートフォースを使ったアプローチでは限界がそのうちくるだろうなという気もしています。
また、標準化のために提出されたアルゴリズムでも指摘を受けて修正されており、ハッシュベースのような（歴史が浅いとはいえ）比較的安全性の解析がしやすそうなスキームでも脆弱性⁸が一部見つかっていることから、暗号の設計の難しさが垣間見えました。

参考文献