はじめに
この記事では論文1の解説を行います。
これまで、このブログでは STARK234やSPHINCS56を用いた、暗号通貨の安全性を保ちつつ履歴を圧縮しうる方法について紹介してきました。
その中で「ハッシュ関数のみに依存した暗号通貨のアーキテクチャ」を考察してきましたが、具体的にハッシュ関数ベースの署名アルゴリズムを圧縮する場合のコストについて今回初めて紹介いたします。
論文の趣旨
論文1ではハッシュベース署名であるLamport+(ランポート署名7の変種)というワンタイム署名アルゴリズムを用意し、この署名検証をSTARKによって行う場合にどのくらい時間がかかるのかを調べています。残念ながらSPHINCSではありません。
前提として、STARKのアルゴリズムで使うハッシュ関数はBLAKE38というハッシュ関数で、内部のハッシュベース署名ではSTARKで処理する際に速度的に有利になるRescueハッシュ9という別のハッシュ関数を使っています。もしSHA-256などの一般的に使われているハッシュ関数を両方で使うと、暗号学的な仮定としては少なくてすみますが、速度やサイズは悪化すると想定されます。
そのため、以下で示す計算時間や消費メモリなどの数値は、あくまでも最善の結果だと考えておいたほうが良さそうです。
論文で示された実行時間や要求RAMの計算結果は、以下の表の通りになります。
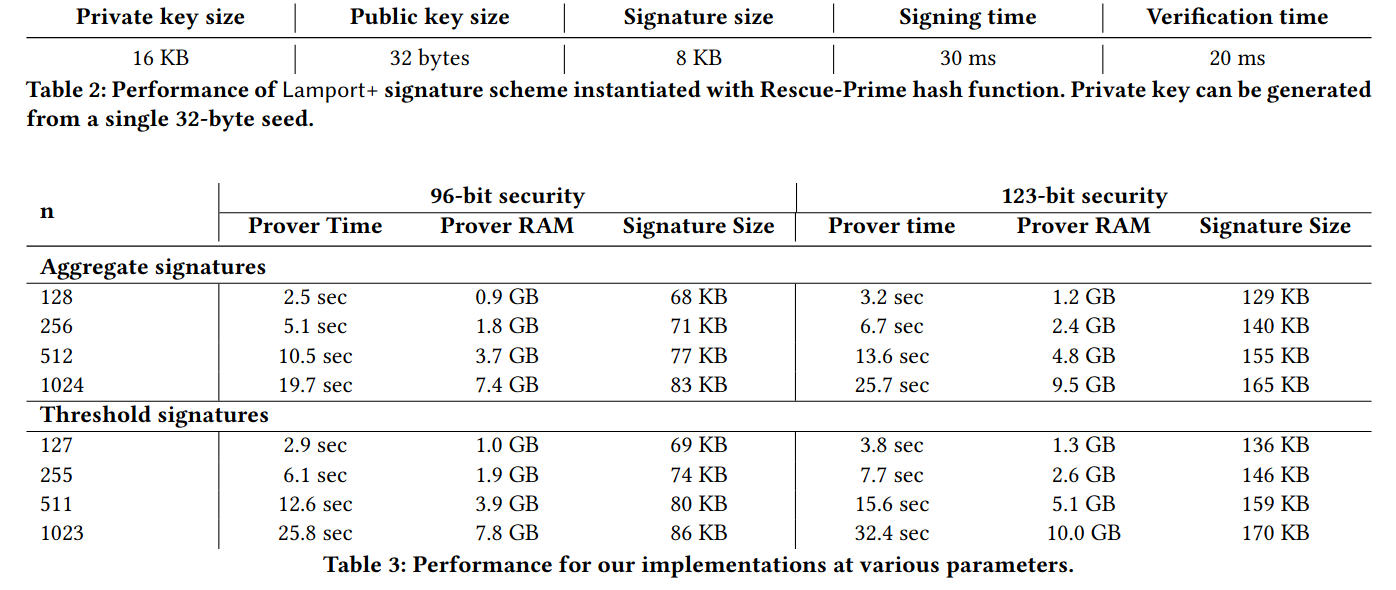
Table 2に書かれているのが単体のLamport+の実行時の署名サイズ、署名計算時間、検証時間です。
Table 3に書かれているのが署名の数を128, 256, 512, 1024個分に増やしたときの、STARK圧縮時間、圧縮計算時のRAM消費量、STARK証明サイズです。
署名の数nが増えるに従って、証明時間とRAM消費量は線形に増えていることがわかります。
考察
STARKによる署名圧縮は十分有効
上記の表から分かるように、1000個のLamport+署名を集めて165 KBということは、一つの署名あたり165バイト程度まで抑えることに成功していることになります。ランポート署名はワンタイム署名であり一回しか署名として使えないのですが、例えばブロックチェーンのコンセンサスレベルで、ランポート署名を複数回使うことを禁止してしまえば、やや不便ではあるものの、安全かつコンパクトな圧縮ができそうです。
1000個では既存のECDSAの署名サイズ(64バイト)には叶いませんが、3000個の署名であれば既存のECDSAの署名サイズに近くなると推定できます。ただ、以下のようなポイントに留意が必要です。
- 常にブロックにトランザクションが多量に入るとは限らない。ブロックにトランザクションが多量に入っていない場合、圧縮をする意味がない
- コンセンサスアルゴリズムの内部で圧縮と証明検証を行う場合、場合によっては圧縮、場合によっては通常の署名検証という形になるが、システムが複雑化しそう
- (IBDの際に)コンセンサスアルゴリズムの外部で圧縮と証明検証を行う場合には複雑化はしなさそう。ただし、その場合巨大なワンタイム署名がブロックに入ることになるためいずれにせよ問題にはなる
- 署名圧縮をブロック生成者(=採掘者)が行う場合、25.7秒という証明時間はマイニングを行う上で障害になるほどに長い
- ただしこれは署名生成自体をASICで行うようになればあまり問題にはならなくなる可能性もある
SPHINCSで同等の署名圧縮を行うのはハードルが高い
SPHINCS+については、検証時に必要なハッシュ実行回数の見積もりが論文10として出ています。論文10のテーブル2によると、大体検証時には最低でも13117回のハッシュ実行が必要です。
Number of blocks of SHA-256 computed in SPHINCS+ -128f-simple
| Function | SHA-256 |
|---|---|
| Key Generation | 4847 |
| Sign | 112937 |
| Verify | 13117 |
ここから考えると、SPHINCSでは128ビットのランポート署名に対して最大でも100倍の計算時間とRAMを消費すると推定できます。論文1の条件でこれを実行しようとすると、40分の計算時間と1TB近いメモリが必要になります。したがって、単純に暗号通貨のコンセンサスアルゴリズムにこの仕組みを導入するのは難しそうです。実際にSPHINCSに対してSTARKを使った圧縮を行う場合には、再帰的なSTARKを使った並列化が必須になると考えられます。
参考
-
Aggregating and thresholdizing hash-based signatures using STARKs https://eprint.iacr.org/2021/1048.pdf ↩ ↩ ↩
-
RISC Zero v1系でzk-STARKによるRustプログラムの証明と検証をする https://tech.hashport.io/4954/ ↩
-
STARKを用いてRISC-Vの実行履歴証明を行うフレームワークRISC Zeroの紹介 https://tech.hashport.io/4512/ ↩
-
FRIプロトコルを用いたSTARKアルゴリズムの紹介 https://tech.hashport.io/3924/ ↩
-
ランポート署名を改良した耐量子署名アルゴリズムSPHINCSの紹介 https://tech.hashport.io/4535/ ↩
-
ハッシュベースの署名アルゴリズムSPHINCSを改良したSPHINCS+(C)の解説 https://tech.hashport.io/4624/ ↩
-
ランポート署名 https://ja.wikipedia.org/wiki/%E3%83%A9%E3%83%B3%E3%83%9D%E3%83%BC%E3%83%88%E7%BD%B2%E5%90%8D ↩
-
Rescue-Prime: a Standard Specification (SoK) https://eprint.iacr.org/2020/1143 ↩
-
Optimization for SPHINCS+ using Intel® Secure Hash Algorithm Extensions https://csrc.nist.gov/csrc/media/Events/2022/fourth-pqc-standardization-conference/documents/papers/optimizatin-for-sphinc-plus-using-intel-pqc2022.pdf ↩ ↩


