論文解説: Fast constant-time gcd computation and modular inversion

Table of Contents

本稿ではこの論文を扱います。
https://gcd.cr.yp.to/safegcd-20190413.pdf

この記事で紹介する内容

電力解析などのサイドチャネル攻撃に対する防衛策として、入力の値にかかわらず一定の時間(constant-time)でGCDを計算する需要がある。ここでいうconstant-timeは入力長nに対してO(1)で実行できるという意味ではない。既存の一定時間での計算アルゴリズムも存在するが、GCDをより高速に計算するアルゴリズムを示す。

GCDを計算するアルゴリズム

基本的にユークリッドのGCDアルゴリズムを用いており、1980年代にBojanczyk, Brent, Kungによって開発されたGCDアルゴリズムと似ている。

特徴として

ケースの区別が少ない
データフローは「条件付きスワップ」と「消去」の二つに分解でき簡単である
反復回数がより少ない
ステップをジャンプすることができる

があげられる。

GCDの高速計算化

この論文においてはGCDの計算を高速化する手段として｢除算ステップ(division steps)」が提案されている。
この除算ステップを一定回数反復すると、入力の gcd や、入力が互いに素の場合のモジュラーなどが明らかになる。
この除算ステップのアルゴリズムをdivstep関数とする。

divstep関数のアルゴリズムは以下の通り:

またその定義は以下のようになる:

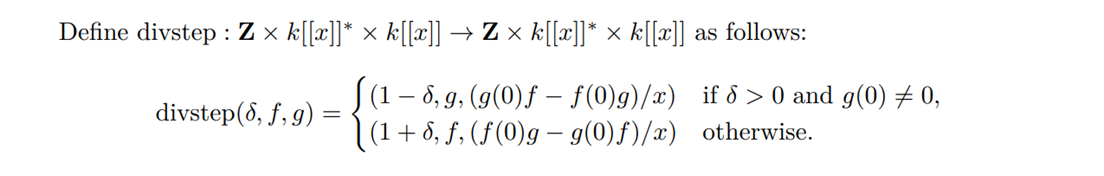
divstep関数は二つのステップに分けられ

$δ > 0$ または $g(0) \neq 0$ のとき $(δ, f, g )$ を $(-δ, g, f )$ に置き換える条件付きスワップ
$(δ, f, g )$ を $(1 + δ, f , (f(0)g - g(0)f)/x )$ に置き換える消去法

の繰り返しである。

除算ステップの反復計算の高速化

$(δ_{n}, f_{n}, g_{n}) = divstepn (δ, f, g)$ までの反復計算の高速化を目指す。

まずdivstepの反復処理を次から次へと計算するアルゴリズムは以下の通り:

これを高速化する手段として以下の二つがある。

定時間計算
除算ステップのジャンプ

定時間計算

一定時間のビット演算に置き換える。これにより入力のさまざまな表現に対して、これらの計算の正確なコストを最小化する。

$ｓ$ を $-δ$ の符号ビットとし、 $δ≧0$ の場合は0を、 $-δ＜0$ の場合は1を意味する
$z$ を $g(0)$ のノンゼロビットとし、 $g(0) = 0$ の場合は 0 を、 $g(0)\neq0$ の場合は 1 を意味する
$1 + (1 - 2sz)δ$ を計算し、出力する
$f \oplus sz(f \oplus g)$ を計算し、出力する。 $sz = 0$ の場合は f、 $sz = 1$ の場合は g を得る
$(1 - 2sz)(f(0)g - g(0)f)/x$ を計算し、出力する。または単純に $(f(0)g-g(0)f)/x$ を計算し、出力する

除算ステップのジャンプ

$n \leq 1$ の場合止める
$j \in {1, 2, . . . , n - 1}$ を選ぶ
jステップ移行行列 $T_{j−1} · · · T_{0}$ を用いて $δ, f, g$ から $δ_{j} , f_{j} , g_{j}$ へとjステップジャンプする
同様に、 $δ_{j} , f_{j} , g_{j}$ から $δ_{n} , f_{n} , g_{n}$ へと、別の n - j ステップジャンプする

具体的にアルゴリズムは以下の通り:

性能

係数が $2^{255}–19$ での最新の速度記録はCPUコアがHaswell、Skylake、Kaby Lake でそれぞれ 11854 サイクル、9301 サイクル、8971 サイクルであったがこのアルゴリズムを用いることで10050サイクル、8778サイクル、8543サイクルと速度が向上した。