はじめに
本記事では、https://eprint.iacr.org/2021/032.pdf
の数理的な部分の解説を行います。
こちらの記事(https://atmarkit.itmedia.co.jp/ait/articles/2111/10/news060.html)
でも、同論文の日本語での解説がなされています。
まず、モチベーションを説明し、プロトコルの説明を実験の解説から、順を追って行います。
最後にまとめを述べます。
モチベーション
これまでの研究での問題
Multi-prover interactive proofs: how to remove intractability assumptions.(M. Ben-Or, S. Goldwasser, J. Kilian, and A. Wigderson. )によるアイデアは、3色塗り分け問題がNP完全問題であるという前提のみから、複数の証明者によるゼロ知識証明の安全性を示せるというものである。
この対話的ゼロ知識証明による三色問題の検証は、直感的には、警察の捜査官(以後の検証者)が取調べを行う際に容疑者(以後の証明者)を別室に連れていき、真相を見極める戦略と同じアプローチを取っている。

このアプローチを採るには、容疑者同士を物理的に隔離した状態、暗号学的に表現すると「the impossibility to communicate(通信不能)」の状態にしなければならない。
特殊相対性理論の原理である「光速より速い信号はない」を仮定し、異なる証明者に同時にクエリを送信すると、物理的に互いの間で信号を送ることができない短い時間が存在することになる。これまで、このような考え方は主に理論的なものであり、既知のプロトコルは証明者と検証者間で非常に大きな情報伝達を必要とし時間がかかるため、実装が不可能だった。
この研究での実証実験の結果
Practical relativistic zero-knowledge for NP.(C. Cr´epeau, A. Massenet, L. Salvail, L. Stinchcombe, and N. Yang.)で提案されたプロトコルの、データ通信量を下げて通信時間を短くし、物理的に400m離した2組の証明者と検証者のペアに対して、実装した。60m離した実験も行った。
その結果、どちらの距離でも実行時間は1秒だった。更にこの結果から、一方向性関数の存在といった計算論的前提に依存せず、3色塗り分け問題のNP完全性と光速を上回ることはないという特殊相対性理論の原理のみを前提にして、NP完全問題(三色塗り分け問題)に対する相対論的ゼロ知識証明の実験的実現が示せた。
プロトコル
実験の解説
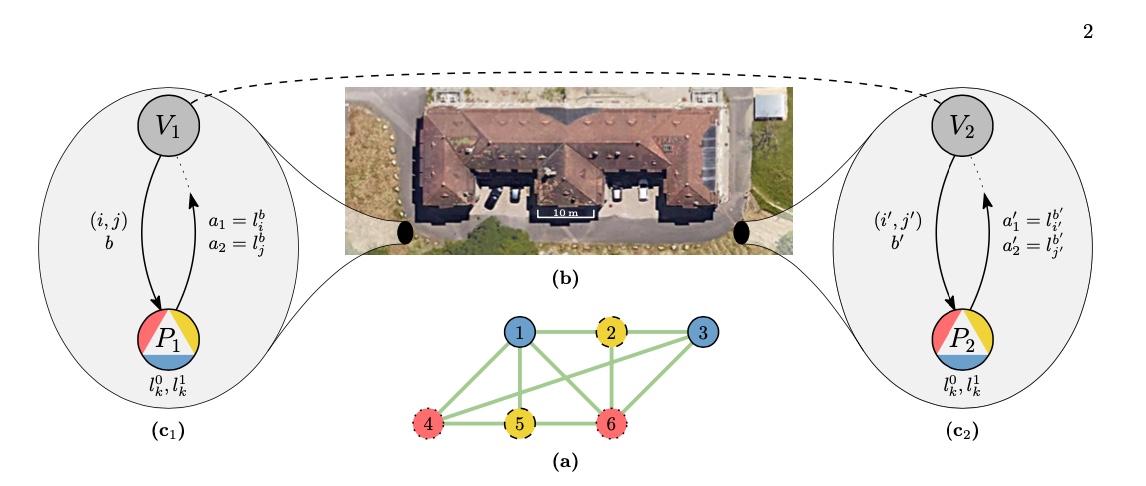
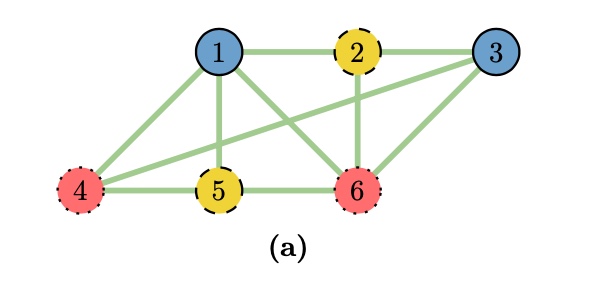
(a)
6個の頂点と10個の辺を持つ3色塗り分け可能なグラフ。
c_1 = c_3 = 0(青一色)、
c_2 = c_5 = 1(黄破線)、
c_4 = c_6 = 2(赤点線)
となっており、辺で結ばれた頂点の色は異なっている。
概略での記法を用いると
頂点k∈\{0, 1, 2,3,4,5,6\}に対して、c_k(n)∈\{0, 1, 2\}
(b)
それぞれのペアの間の距離は60m、つまり光速で200ナノ秒である。この距離のため、この時間スケールでは特殊相対性理論により2つの証明者間の通信は不可能である。検証者は、光ファイバーによって、同時に証明者に質問を発する。
(c)
検証者-証明者ペアのプロトコルの1ラウンドの説明図。
各検証者V_1,V_2はビットbと辺を証明者P_1,P_2に送る。
(V_1 \rightarrow P_1、V_2 \rightarrow P_2)
証明者P_1,P_2はその辺の端点でb番目のラベルを答える
(P_1 \rightarrow V_1、P_2 \rightarrow V_2)。
すべての頂点kについて、証明者は2つのラベルl^k_0 , l^k_1 ∈ \{0, 1, 2\}について事前に合意しており、その合計は3色、すなわちl^k_0+ l^k_1 ≡c_k (mod 3) にならなければならない。両側の同じ辺と反対側のビットを尋ねるとき、検証者はラベリングの定義から、グラフが3色であることを証明者が知っていることを確認することができる。
検証者が不正をしていないことを確認するために、検証者は(少なくとも)1つの頂点を共有する辺と同じビットを送信することもできる。この手順を何度も繰り返すことで、検証者は不正な証明者がプロトコルを通過する確率を任意に小さくすることができる(健全性)。しかし、すべての証明者の回答が手元にある状態でも、検証者は当初より3色のカラーリングを複雑にすることはできない(証明者から流出する知識がゼロであるということで、ゼロ知識性という)。
概略
頂点の有限集合Vと辺の集合体Eで(V, E)を有限無向グラフとする。
さらに、このグラフは3色である(図1(a)参照)。以下では
ここでは、3色つの異なる色を0,1,2と表記する。
プロトコルは、後述する適切な方法で配置された2つの検証者と2つの証明者を含む。
最初に、2つの証明者は、頂点k∈Vとラウンドを示すnに対してランダムな3色塗り分けc_k(n)∈\{0, 1, 2\}を事前に知っている。
以下では、簡潔にするため、各ラウンドnの従属性は省略する。
以下、3色塗り分け問題のルールである。
すべての頂点kに対して、l^0_k+l^1_k ≡ c_k(mod 3)が成り立つような2つのラベリングl^0_kとl^1_kを選ぶ。
なお、適切なカラーリングとは逆に、ラベリングl^0とl^1は隣接する頂点で異なる値を持つ必要はない。
ラウンドは図1(c)に示すように
(i)各検証者がその証明者に
辺 (i, j) ∈ E とビット b ∈ {0, 1}を送信し
(ii)各証明者はl^b_i,l^b_jを各検証者に回答し、
(iii)2人の検証者がチェックする。
次の2つの段落で説明するように、証明者の回答は どの当事者もプロトコルを中止しない場合、ある安全レベルに達するまでラウンドを繰り返す。
検証者のテストは2つの異なる成果を得られる。
一方では、検証者は、
3色塗り分け可能なグラフかどうかを証明者が本当に知っているか、検証できる。
このテストは、両検証者がそれぞれ
同じランダムな辺e=(i,j)=(i', j') = e' ∈Eと
b \not =b'を送信したときに、
証明者の解答たる(a_1 ,a_2)と(a'_1 ,a'_2)が
a_1 + a'_1 \not ≡a_2 + a'_2(mod 3)の時に限り受理されるから、
実行できる。
一方、検証者は証明者の答えの一貫性をテストすることができる。
送られた辺が少なくとも1つの頂点(例えば、i=i') を共有し
送信されたビットが等しい(b=b')
とき、2つの証明者の対応する答えが等しい場合(a_1=a'_1)にのみ受理する。
これにより、通常、証明者が
質問された辺を無視するような方法で回答するのを防げる。
完全性
グラフが3色塗り分け可能かつ、正直な検証者と正直な証明者では、必ず受理される。このようなプロトコルの性質を完全性と呼ぶ。
健全性
正直な検証者と不誠実な証明者の場合(グラフが3色塗り分け可能でない場合)、健全性とは、
「検証者は、何ラウンドも行うことで、非常に高い確率で不正を明らかにすることができること」をいう。
直感的には、V_1の質問より前に、もしある証明者(例えばP_2)の回答が、ペアの検証者(V_2)に送信されたならば、V_1のP_1への質問を知らずに回答したに違いない。
検証者同士を十分な距離で分離し、慎重にプロトコルのタイミングを計ることで、特殊相対性理論を利用することができる。
この分離を作ることで、古典的な計算機である証明者に対して健全であるプロトコルを実現することができる。
ゼロ知識性
不誠実な検証者と、正直な証明者にとって
ゼロ知識という性質は、検証者が何の情報も得られないということになる。
上記のプロトコルはこの性質を満たしている。
データ通信量の削減
以下のプロトコルの、検証を行う(iii)フェーズで、通信量を削減している。
まず、文献で提案されたゼロ知識証明を思い出してみよう。[12].
最初に、2つの証明者は、ランダムな3色カラーリングc_k(n) \in \{0, 1, 2\}とk ∈ Vに対して無作為抽出者b_k(n) ∈ \{0, 1, 2\}とラウンドを表すnを事前に。
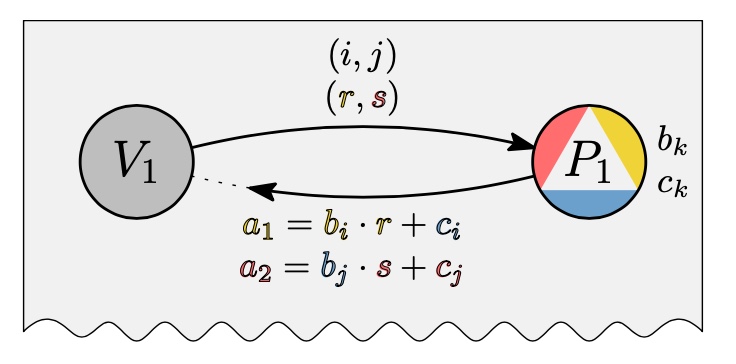
ラウンドは上図に示すように、
(i)各検証者が証明者に辺(i,j)=e∈E と
2つの無作為抽出者 (r, s) ∈ \{1, 2\}を送信する。
(ii)それぞれの証明者はa1 ≡ b_i ・ r + c_i(mod 3)、a2 ≡ b_j ・ s + c_j(mod 3)を返答する。
(iii)2つの検証者がそれぞれの証明者の答えを検証する。
削減前の検証
2つの検証者が同じ辺e=(i,j)=(i', j') = e' ∈Eと
無作為抽出(r',s')=(-r,-s)を送信したときに、
証明者の解答たる(a_1 ,a_2)と(a'_1 ,a'_2)が
a_1 + a'_1 \not ≡a_2 + a'_2(mod 3)の時に限り受理される。
また、検証者は証明者の答えの一貫性をテストすることができる。
送られた辺が少なくとも1つの頂点(例えば、i=i') を共有し
送信された無作為抽出者が等しい(r=r')
とき、2つの証明者の対応する答えが等しい場合(a_i=a_i')にのみ受理する。
これにより、通常、証明者が
質問された辺を無視するような方法で回答するのを防げる。
削減後の検証
Practical relativistic zero-knowledge for NP.(C. Cr ́epeau, A. Massenet, L. Salvail, L. Stinchcombe, and N. Yang.)では、検証者のための以下の戦略が示されている。
が与えられる。(r, s) ∈ \{1, 2\}まず、辺(i, j)と無作為抽出者(r, s)を指定する。
次に、確率1/5で、辺は等しくなり((i', j')=(i,j))かつ(r',s')=(-r,-s)を満たすように選択する。
また、確率2/5で、r'=r,i'=i,(i',j')\in Eを満たすように選択する。
また、確率2/5で、s'=s,j'=j,(i',j')\in Eを満たすように選択する。
すると、交換されるデータ量は、従来のプロトコルに比べて非常に少ないことがRelativistic (or 2-prover 1-round) zero-knowledge protocol for NP secure against quantum adversaries. (A. Chailloux and A. Leverrier.)から、
削減前のデータ量は頂点の数|V|の多項式であるのに対し、削減後では|V|の対数だけで表わせることが判明している。この特徴により、大きなグラフであっても通信時間が短いため、検証者と検証者のペア間の距離を短くすることができる。
グラフ
以下の実験で使用したグラフは|V|=588頂点、|E|=1097辺であり、広く安全とされているk=100のセキュリティパラメータに達するには約100万ラウンドが必要である。
実装
通信速度の向上を主眼としている。
証明者側をフィールドプログラマブルゲートアレイ(FPGA)上で動作させることにより、通信レイテンシ、計算の高速化、そして時間的な信頼性を向上させた。検証者側では、通信にFPGAを用いると共に、グローバルな監視とチェックのための標準的なコンピュータを用いた。
この実験には2つのタイムスケールがある。
証明者同士、検証機同士の通信時間とラウンドの繰り返し時間である。
前者は、両者間の必要最小距離を定めるもので2つの場所の計算速度によって制限される。
後者は、証明者側の時間を決定する。
400mの場合
検証者-証明者ペアを2組用意し
キャンパス内の異なる建物に、1.3 µsの時間間隔に相当する390m離れて配置する。
同期には、GPSクロックを使用する。
両検証者はペアの証明者に課題を0.3MHzの周波数で送信し、証明者は課題を受信すると、その回答を計算する。
使用するシステムの精度の低さを考慮すると、検証者の課題が発行されて証明者の解答の受信完了までの経過時間は840ナノ秒で、当事者間の時間間隔1.3μsを下回っている。
そのため、健全性の要件を満たしている。
100万ラウンドのプロトコルの実行時間は約3秒である。
検証者が検証する時間は、840ナノ秒で、理論上の最小距離は250mと決まっている。
この単純なプロトコルに基づいて、250m以上離した場合の設計ができる。
60mの場合
60m離れて配置されている(200nsの時間間隔に相当)場合では、以下の通り。
2つの検証機の間でトリガ信号が変化する。2台目の検証機でトリガーを捕捉すると、2台目の検証機は接続されている証明機に課題を送信する。第一検証者は、トリガーが第二検証者に転送されるまでの時間、課題の送信を遅らせる。したがって、両方の検証者は、隣接する証明者に課題を送信する。この場合も、検証者は課題を受信するとすぐに、共有データに基づいて答えを計算し、検証者に送り返す。このため、検証者は最短で57.6 mの距離にいる必要がある。繰り返し周波数が3MHzの場合、100万ラウンドのプロトコルは1秒未満で実行される。
また使用したハードウェアとその時間およびメモリの制限により、同じセキュリティパラメータk=100と適度な総時間(約3秒)を維持しながら、グラフのサイズを1桁大きくすること、すなわち|V|〜5000および|E|〜10000が可能である。
まとめと感想
データ通信量を下げて通信速度を早くして、特殊相対性理論の原理の前提を活かせるようにプロトコルを改良して、3色問題のゼロ知識証明の実験的実現を示すという面白い論文でした。
ブロックチェーンシステムやスマートコントラクトといった、ゼロ知識証明の概念が関連する幅広い分野で応用される可能性があるとのことです。
参考文献
日本語での解説
相対性理論でITのデータ転送を保護、どうやって?
3色問題のゼロ知識証明のプロトコル
Practical relativistic zero-knowledge for NP.(C. Cr ́epeau, A. Massenet, L. Salvail, L. Stinchcombe, and N. Yang.)
3色問題のゼロ知識証明のプロトコルで、本論文が採用した検証方法により、データ通信量が削減できることを示した論文
Relativistic (or 2-prover 1-round) zero-knowledge protocol for NP secure against quantum adversaries. (A. Chailloux and A. Leverrier.)
3色性の非常に難しいインスタンスに対応する大きな臨界グラフを構築するアルゴリズムを提案した論文
Constructive generation of very hard 3-colorability instances.(K. Mizuno and S. Nishihara.)