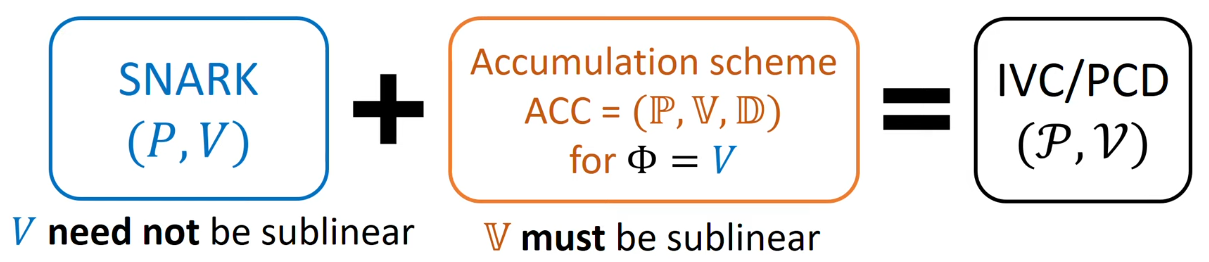第三者を信頼せずに段階的検証可能計算(IVC)を実現するHaloの解説

Table of Contents

概要

この記事では再帰的SNARKを利用したIVC/PCDのフレームワークであるHalo2の解説を行います。
Halo2とは、暗号通貨Zcashの開発母体であるElectric Coin Company(ECC社)で開発されたIVC(Incrementally verifiable computation), PCD(Proof carrying data)の実装です。その他の実装と比較するとトラステッドセットアップが不要という特徴があります。

Halo2は以下のような構成要素からなります。

アキュムレータを用いた再帰的SNARK[1]
SNARK の実装 (Plonk) [2]
Plonk内で使われる多項式コミットメント(Polynomial Commitment Scheme; PCS)

この記事では主に1を解説します。2と3についてはそれぞれ別の記事で解説するので、そちらを参考にしてください。

理論上はともかく、実際の計算機にて計算を行う上で実装に際して様々なハードルがあります。それらの最適化まで含めて解説しますが、[9]のようなPCDを使った具体的な応用までは解説しません。

小史

IVC/PCD

歴史的にはIVC[5][8]が2008年に提案され、PCD[6]がその一般化として2010年に提案されていますが、効率的な実装は存在しないままでした。

SNARKを用いたIVC/PCD

SNARKはその定義から言って、検証される証明サイズが小さい証明システムです。したがって、SNARKの証明検証ロジックで使われるプログラムを、別のSNARKで証明の対象にすることができます。これをつなげることで「誰かが検証した証明付きデータを、さらに加工した」ということを証明付きデータとして再帰的に生成することができます。
ナイーブにこれをやる場合、すべての計算途中のデータと追加計算が正しいことの証明を積み重ねていけばいいはずです。しかし、上記のような再帰的なSNARKを使うと、計算途中のデータを捨てて最終的な証明とデータだけを見て途中の計算過程が正しいかどうかを判定する証明システム(IVC/PCD)を構築することができます。
これを2012年に最初に提案した論文が[4]です。

この実装に際して、楕円曲線ペアを用いることで効率的な実装を行えるようにした2014年の論文が[7]です。

歴史的には、ここまでで効率的なSNARKを使ったIVC/PCDは一旦実現していますが、それらはすべて非効率であるか、トラステッドセットアップが必要なものでした。

トラステッドセットアップ不要なIVC/PCD (Halo/Halo2)

トラステッドセットアップが必要な原因は、主に効率的なSNARKを作ろうとすると避けて通れないPCSの実現方法にあります。PCSには様々なものがありますが、その中には効率的だがトラステッドセットアップが必要なKZGコミットメントと呼ばれるものがあります。それとは別に、内積アーギュメント(Inner Product Argument; IPA)を使ったBulletproofsのような仕組みを使ったPCSもありますが、それは検証時間がサブリニアではなく再帰的SNARKでは使えません。

後者の、IPAを使ったPCSをSNARK証明アルゴリズムの中で使うと、検証時間のサブリニア性を満たさず通常のPCD/IVCをそのまま実現することができません。
では、そのような 検証時間のサブリニア性を満たさないSNARKを使っても、サブリニア性を満たすSNARKと同じ様にIVC/PCDを構成することはできるでしょうか？

上の疑問を肯定的に解決するHalo/Halo2というプログラムが構想され公開されました。

HaloではIPAの検証をバッチ化（＝アキュムレータ化）できる性質を用いています。

そして、Haloのアイデアを一般化したアキュムレーションというスキームを導入することによってさらにIVC/PCDの構成を改良し、SNARKの検証部分の計算を一度だけ行うようにしたものが[1]です。[1]ではこれまでの「SNARKであっても検証時間がサブリニアでなければIVC/PCDには使えない」という条件を緩和してIVC/PCDに使えるSNARKのクラスを拡大しています。

再帰的SNARKを使ったアキュムレーション付きPCD/IVC[1]をこの記事で扱うまでに積み重ねられた研究は以上のような歴史があります。

解説

再帰的SNARKによるIVC/PCD

主に[4][7]の解説。
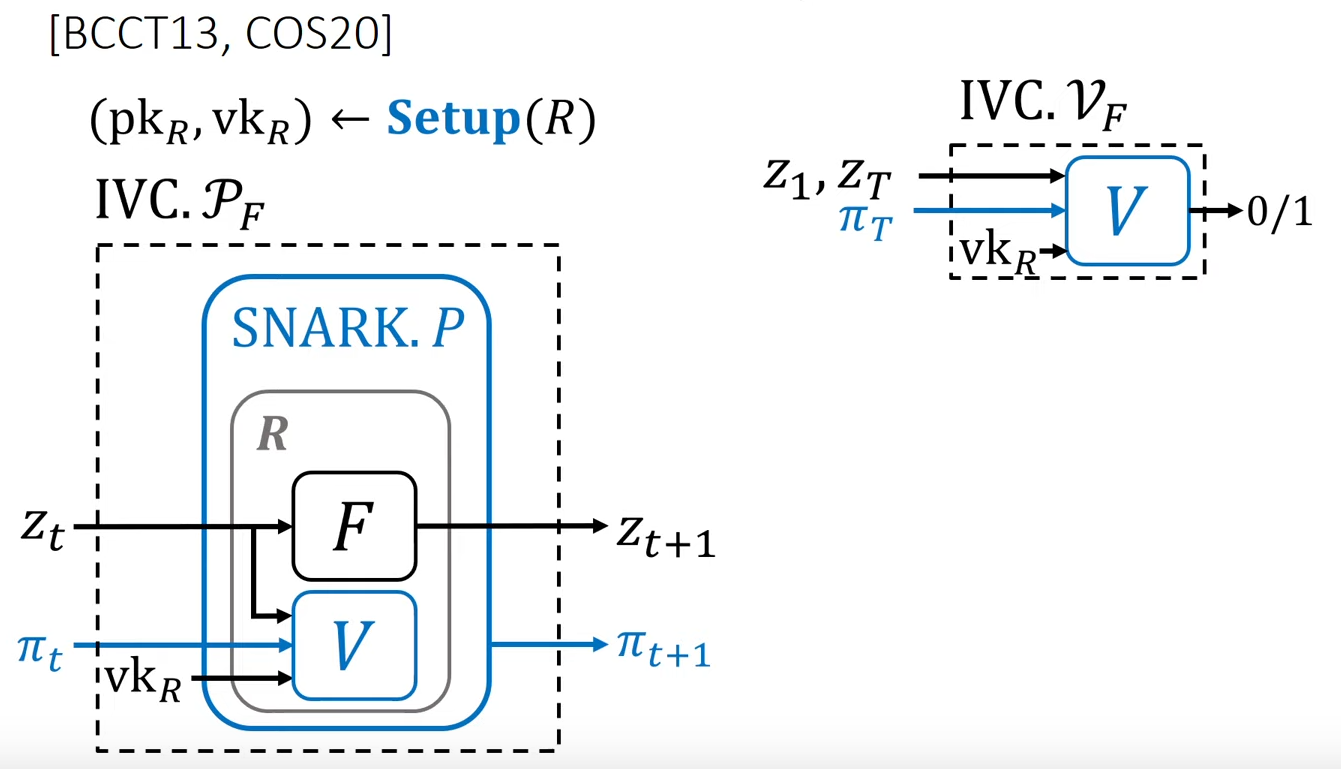
t番目時点の計算におけるIVCの状態 $z_t$ 、証明 $\pi_t$ 、証明鍵 $pk_R$ 、検証鍵 $vk_R$ を仮定する。またIVCの検証者による最終状態 $z_T$ 、最終状態の証明 $\pi_T$ とする。

以下は[11]から持ってきた図である。関数Fに対するIVCの証明アルゴリズム( $\text{IVC.P}_F, \text{IVC.V}_F$ )をSNARKの証明アルゴリズム $\text{SNARK.P}$ と $\text{SNARK.V}$ を用いて構成している。

この図は以下のような順番で読む。

証明者による計算

状態 $z_t$ は関数Fによって加工され、 $z_{t+1}$ となる。
状態 $z_t, \pi_t, vk_R$ を $\text{SNARK.V}$ に通して計算することで、一つ前の状態が正しいということを検証できる。
2のFと $\text{SNARK.V}$ をまとめてRという回路を作る。これは1と2を同時に行う回路となる。
$\text{SNARK.P}$ は公開されている回路Rに対し $z_{t+1}$ を出力とするような入力 $z_t, \pi_t, zk_R$ が存在することを証明する。この結果として $\text{SNARK.P}$ が生成する証明が $\pi_{t+1}$ である。

検証者による計算

$\text{SNARK.V}$ が $z_T, \pi_T, vk_R$ を使って状態が正しいかをSNARKによって検証する。

IVCの完全性はSNARKの完全性より従う。また、健全性はSNARKの知識健全性によって再帰的に一つ前の証明からの知識抽出可能性があることから従う。
ただし、 $\text{SNARK.V}$ の検証時間は回路Rの実行時間に対して線形以下（サブリニア）でなければならない。さもなければ、次ラウンドではRの実行よりも前のRの検証に時間がかかってしまい、 $\text{SNARK.P}$ による証明時間が増大していってしまう。（そもそもRの定義から言ってR自身の検証回路が自分自身に含まれているので、この定義を満たすためには $\text{SNARK.V}$ の検証時間が回路Rの実行時間よりも小さい必要がある）

以上、 $\text{SNARK.P}$ の中に $\text{SNARK.V}$ を入れる具体的な構成が可能なのかという疑問はあるが（検証用のサーキット自体は汎用的なものとしておき、そこに検証用の鍵を引数として渡すような実装とすることで実現しているらしい）、それだけ克服すれば問題なくIVCが実現されることが理解できると思われる。

アキュムレータを用いた再帰的SNARKによるIVC/PCDの実現

主に[1]の解説。
以下は[11]から持ってきた図。

検証時間が回路Rに対してサブリニアではないようなケースに対しても、アキュムレーションスキームの検証時間がサブリニアであればIVC/PCDが成立する。

アキュムレーションスキームとは以下の図のようなスキームのこと。

アキュムレータと呼ばれる値 $a_i$ が存在し、各ステップ前後での値を記録していく。(具体的にはhaloでは $a_i$ はIPAの圧縮された証明であり、2つのIPAの証明を同じサイズの1つのIPAの証明に圧縮することができるという性質を利用している。)
最終的に決定アルゴリズム(Decider; D)というアルゴリズムがアキュムレータの値を検証し、その値が正しければこれまでのアキュムレータで記録された値を検証するアルゴリズム(上図のV)がすべて1であると言えるような性質を持つ。(具体的にはhaloではDはIPAの検証器となる。)
このようなアキュムレーションスキームを効果的に成立させるにはアキュムレーションスキームの $V$ (具体的にはhaloにおいては $V$ とはアキュムレータが正しく加算されていることの証明であり、Dよりも計算コストが軽い)の計算コストが元の $\Phi$ の計算コストよりも小さくなることが必要である（そうでないならば、わざわざDを外に切り出さずにアキュムレータを使わない再帰的SNARKをすれば良いことになるのでアキュムレータを使用する意味がない）。
実際のSNARKベースのIVCを構成する際には、このような $\Phi$ としてはSNARK検証者の $\text{SNARK.V}$ が使われることになる。

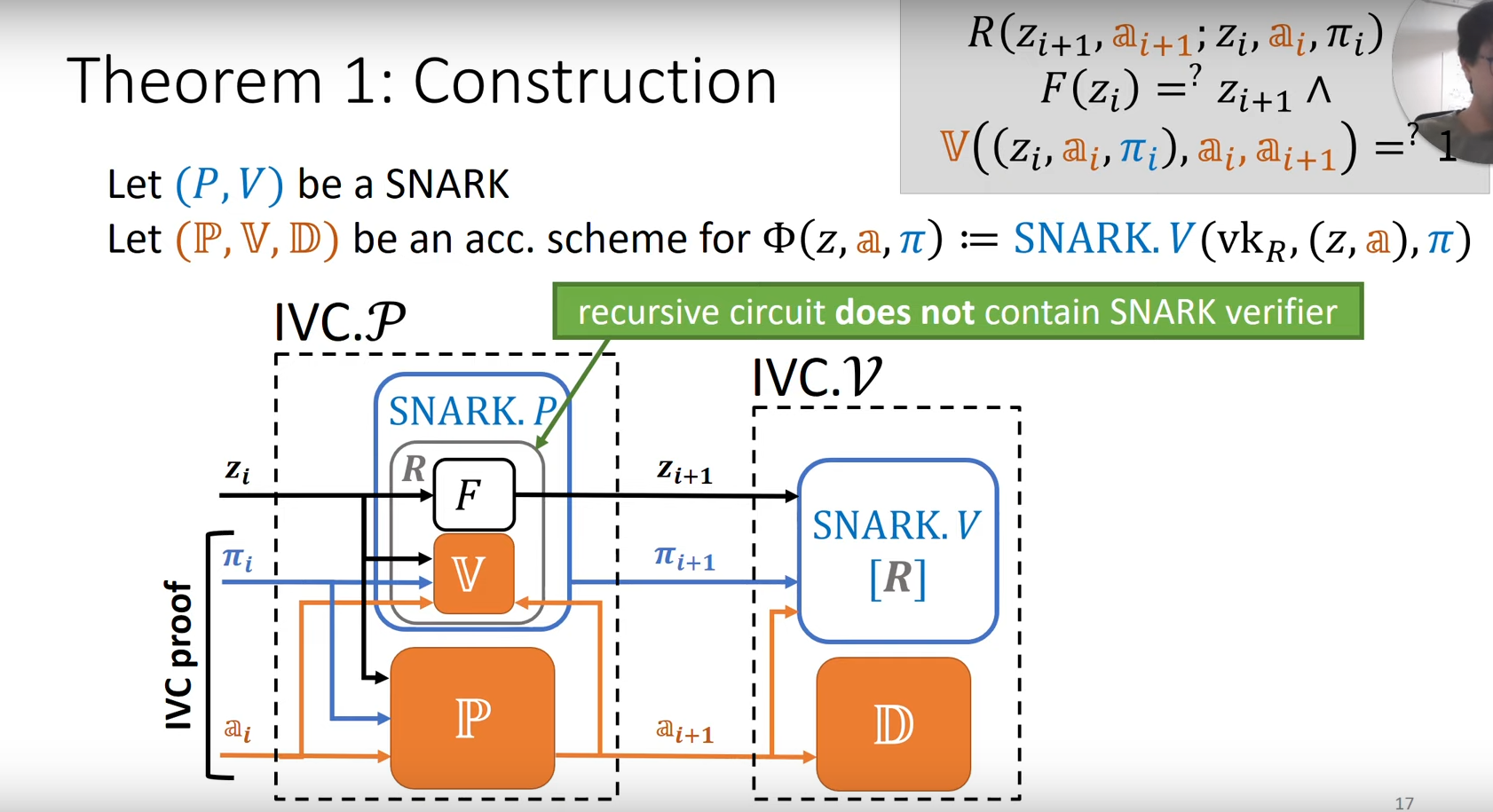
実際に以下の図のようにアキュムレータを含んだ形でIVCを構成する。
各記号は「再帰的SNARKによるIVC/PCD」に依っているのでそちらを参照。

証明者による計算

$z_i$ を元にFを適用して新しい状態 $z_{i+1}$ を生成する。
$a_i, z_i, \pi_i$ を元にアキュムレーションスキームの証明関数Pを通して新しいアキュムレータの状態 $a_{i+1}$ を計算する。
$a_i, a_{i+1}, \pi_i, z_i$ を元にアキュムレーションスキームの検証関数V(SNARK.Vとは別物)を通してアキュムレータの状態を検証する。
「再帰的SNARKによるIVC/PCD」同様にF, Vをまとめて計算する部分を回路Rとする。Rの定義は図の右上にある通り、FとVが正しく計算されているかを確認する回路になっている。
Rを満たす入力 $a_i, a_{i+1}, \pi_i, z_i$ と出力 $z_{i+1}$ が存在することの証明をSNARKにて行う。ここでSNARK.Pを用い、証明として $\pi_{i+1}$ が生成される。

検証者による計算

最終的に $z_T, \pi_T, a_T$ を使ってSNARK.Vを実行する。(SNARK.Vでは存在証明だけを検証するので $a_i$ は不要)
また、アキュムレータの決定アルゴリズムDを実行する。

以上が両方とも検証に成功する場合のみ受理する。
Halo/Halo2におけるアキュムレータは未検証のIPAの証明をバッチ化したものであるということができる。
IPAの証明は複数の証明をまとめてサイズを小さくすることができる性質があるため、これをアキュムレータとして使うことができる。これは [1]の「Accumulation scheme for the IPA」で詳しく説明されている。

なおHalo/Halo2におけるアキュムレータの具体的な構成については、詳しくは別記事[15]にて解説する。

再帰的(S)NARKで使われる楕円曲線ペア

主に[7][10]の解説。

上記のようにSNARKの証明アルゴリズムの中で検証アルゴリズムを動かそうとするとき、数学的には楕円曲線上の演算を多用することになる。楕円曲線上の点における「接線を引いて符号を反転する操作」[16]は群をなし、その群の位数はpであるとする。一方で、その楕円曲線自体が定義されている体にも標数が存在し、それがqであるとする。

このときpとqは必ず異なる数字になることが知られている。例えば、ビットコインで使われているsecp256k1という楕円曲線においては
q = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F (115792089237316195423570985008687907853269984665640564039457584007908834671663)
であり、
p = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141 (115792089237316195423570985008687907852837564279074904382605163141518161494337)
であるから、 q > p である[14]。

従って $F_q$ によって $F_p$ を表現することはできるが、 $F_p$ によって $F_q$ を直接表現することができない。なので、整数を分割して $F_q$ 上の演算を $F_p$ 上の演算として扱えるように符号化する必要がある。これは理論上不可能ではないが、実用的ではない。

そこで考えられたのが[7]の楕円曲線ペアを使うアイデアである。以下を満たす2つの楕円曲線のペアを考える。

楕円曲線 $C_1$ の定義されている体の標数がqであり、その点の演算がなす群の位数がpである。
楕円曲線 $C_2$ の定義されている体の標数がpであり、その点の演算がなす群の位数がqである。

以上のような都合のいいp,qを持つ楕円曲線のペアを見つければ、以下の図のようにそれらが互いに証明を相互参照することによって効率的に証明・検証を実行できる。
以下は[10]のスライド。

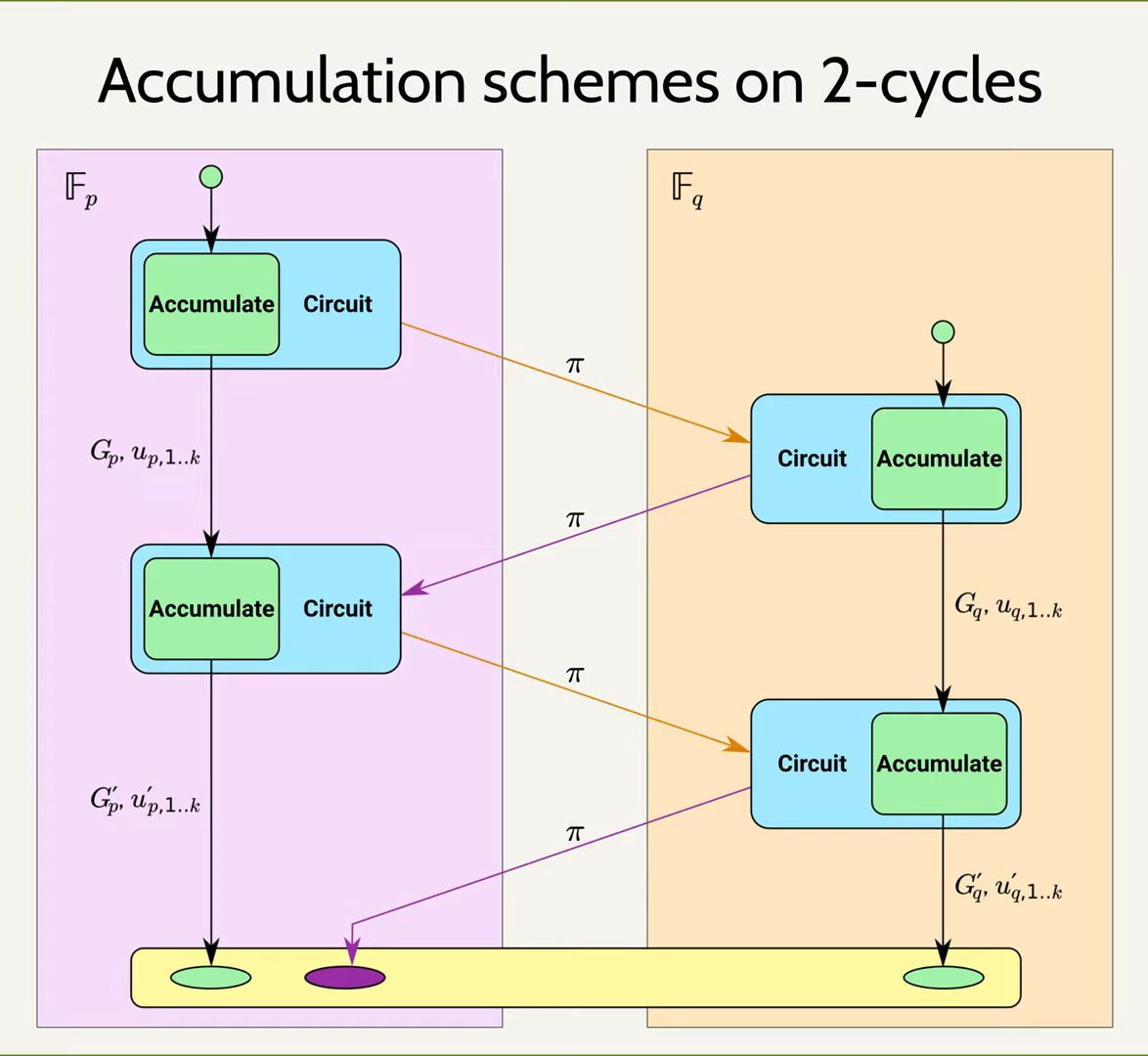
なお、このような性質を持つ楕円曲線ペアはsecp256k1などと同程度に安全であることが期待されているが、厳密には異なる安全性の仮定を導入していることに注意する。

当初[7]ではこのような仮定を満たすものとして MNT4/MNT6 曲線（宮地-中林-高野曲線）ペアが提案された。
Haloでは [13]にあるようなトゥイードルダム・トゥイードルディー(Tweedledum/Tweedledee)という名前の曲線を採用している。

Halo2のために最適化されたPlonkのサーキットとゲート

主に [10]の解説。
[2]で説明されているSNARK(plonk)は一般的な演算の証明を行うことを目的としている。そのため加算ゲートと乗算ゲートを使って演算を算術回路として表現していた。
一方で、実際のHaloではSNARK証明回路の中にSNARK検証回路が含まれる構造になっているため、主なタスクとして実行したいことが予め決まっていることになる。
すなわち、SNARK検証回路の中で頻出する演算を最適化しておくことで、より高速な実行が可能になることが期待される。
まずSNARKの検証では連続した乗算が頻発するので2つの数の乗算ではなく3つの数の乗算をゲートとして導入する。また、乗算では通常のモンゴメリラダー[3]ではなく、よりR1CSの条件式数が少なくなるような改良型のアルゴリズムを使う。
また、フィアット・シャミア変換を使用して対話的証明を非対話証明に変換する演算も多く登場するため、ハッシュ関数(Sinsemilla等)の計算を効率化するアルゴリズムも導入される。
このように、再帰的SNARKの検証を行うHalo2に合わせた工夫がなされている。

まとめ

Halo2の画期性は、(1)トラステッドセットアップ不要で(2)現実的に実行可能なIVC/PCDのフレームワークを作り上げた点にあります。
上記を実現するために本稿で紹介したような様々なテクニックを使用しています。
なお [17]にある通り、現在ユーザー向けのrustによるIVC/PCDのフレームワークは開発中であり利用できない状態です。
新しい論文であるため安全性の検証には時間を要すると思われます。現状では再帰を使わない単純なアプリケーションしか作れないですが、これが引き続き最適化されていくと実用的でより複雑なアプリケーションの基礎になると思うので、楽しみです。