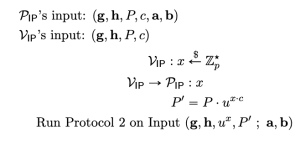はじめに
この記事ではベクトルの値そのものは知らせずに、内積の値が特定の値となるような2つのベクトルを知っていることの証明を送ることができる、内積アーギュメントの一つ、Bulletproofsについて解説します。
検証を入力の長さの対数回のラウンド数で行うことができる点が特徴的です。
この内積アーギュメントを利用することである値が特定の区間に含まれることを、その値そのものを秘密にしたまま伝えるRange Proofやzk-SNARKプロトコルの構成で用いられる多項式コミットメントを実現することができます。
証明の目標
以下\mathbb{G}を位数pの巡回群(例えば有限体上の楕円曲線の有理点のなす群)、\mathbb{Z}_pをpを法とする剰余類環とします。
また\braket{\vec{a},\vec{b}}をベクトル\vec{a},\vec{b}の内積、ベクトルの累乗\vec{g}^{\vec{a}}を要素ごとの累乗の積\prod_{i=1}^n g_i^{a_i}= g_1^{a_1} \cdots g_n ^{a_n}とします。
このプロトコルでは証明者がc\in \mathbb{Z}_pと生成元g,h\in \mathbb{G}^nを検証者と共有した上で
P = \vec{g}^{\vec{a}}\vec{h}^{\vec{b}}\land c = \braket{\vec{a},\vec{b}} \;\;\;(1)
の関係式を満たす\vec{a},\vec{b} \in \mathbb{Z}_p^nを知っていることを証明します。
この証明は新たな\mathbb{G}の生成元u\in \mathbb{G}とコミットメントP \in \mathbb{G}を共有して
P = \vec{g}^{\vec{a}}\vec{h}^{\vec{b}}u^{\braket{\vec{a},\vec{b}}}\;\;\;\;\;\;(2)
を証明するプロトコル(Protocol 2)を用いた下図のプロトコル(Protocol 1)によって証明を行うことができます。
以下(2)の関係を示す証明プロトコル(Protocol 2)を定義します。
この証明は内積
\braket{\vec{a},\vec{b}}を伝えるためのものとしては冗長に思えますが以下で説明する分割統治法を用いたアルゴリズムによって効率的に証明を行うことができます。
証明のプロトコル
上で述べたようにこの証明プロトコルでは分割統治法を利用します。
このプロトコルをまとめたのが以下の図です。
証明の手順は以下の様になります。
(a)
n=1のときn=1のとき証明したいベクトルや生成元のベクトル\vec{a},\vec{b},\vec{g},\vec{h}はいずれもスカラー値a,b,g,hなので証明者はa,b \in \mathbb{Z}を送り、検証者がc = a\cdot bを計算して
g^ah^bu^{c}\stackrel{?}{=}Pを検証することで証明できます。これはPedersen Commitmentです。
(b)n>1のとき
証明者は(2)
を満たす\vec{a},\vec{b} \in \mathbb{Z}_p^nを知っていることの証明を\vec{a},\vec{b}より短いベクトルに対する
別の二つのコミットメントの証明を用いることで再帰的に行います。
証明者はベクトル\vec{a}と\vec{b}をそれぞれ次元が半分の二つのベクトルに分割して\vec{a} _L = \vec{a} _{[:n/2]},\vec{a} _R = \vec{a} _{[n/2:]}と\vec{b} _L = \vec{b} _{[:n/2]},\vec{b} _R = \vec{b} _{[n/2:]}とします。
生成元\vec{g}と\vec{h}も同様に分割し\vec{g}_L,\vec{g}_Rと\vec{h}_L,\vec{h}_Rとします(これは証明者、検証者共に共有している)。
そして証明者はc_L=\braket{\vec{a}_L,\vec{b}_R},c_R=\braket{\vec{a}_R,\vec{b}_L}と置いた後、新たなコミットメントとして
\vec{a}_{L},\vec{b}_{R}に対するコミットメント:L = \vec{g}_R^{\vec{a}_L} \vec{h}_L^{\vec{b}_R} u^{c_L}
\vec{a}_R,\vec{b}_Lに対するコミットメント:R = \vec{g}_L^{\vec{a}_R}\vec{h}_R^{\vec{b}_L}u^{c_R}
の値を計算して検証者に送ります。
証明者と検証者はこの二つのコミットメントが正しいことの証明を再帰的に行い、
上の関係式を満たす\vec{a}_R,\vec{a}_L,\vec{b}_R,\vec{b}_Lを証明者が知っていることを検証者が受理した上で(この時点で受理されなければ証明は拒否される)
検証者はランダムな値x \in \mathbb{Z}_pをチャレンジとして送ります。
その後証明者は新たなベクトル\vec{a}'=\vec{a}_L\cdot x+\vec{a}_R\cdot x^{-1}, \vec{b}'=\vec{b}_L\cdot x+\vec{b}_R\cdot x^{-1}\in \mathbb{Z}_p^{n/2}を計算し、元の\vec{a},\vec{b}に対するコミットメントPと生成元のベクトル\vec{g}, \vec{h}の代わりに
\vec{a}',\vec{b}'に対するコミットメントP' = L^{x^2}PR^{x^{-2}}\in \mathbb{G}と生成元のベクトル\vec{g}' = \vec{g}_L^{x^{-1}} \vec{g}_R^{x}, \vec{h}' = \vec{h}_L^{x^{-1}} \vec{h}_R^{x}を証明者と検証者が共有し、証明者がベクトル\vec{a}', \vec{b}'の値を知っていることの検証、すなわち検証者は\vec{g}^{'\vec{a}'}\vec{h}^{'\vec{b}'}u^{\braket{\vec{a}',\vec{b}'}}\stackrel{?}{=}P'を検証します。
つまり\vec{a},\vec{b} \in \mathbb{Z}_p^nの証明を長さが2組の次元が半分のベクトル\vec{a}_L,\vec{b}_Rと\vec{a}_R,\vec{b}_Lの証明に帰着させています。
計算量とその改善
上のプロトコルをそのまま適用し全てのラウンドで生成元のベクトルを計算し直すと第jラウンド目では\vec{g},\vec{h}それぞれ\frac{n}{2^{j-3}}ビットの生成元の計算を行うので合計の計算量は\sum _{j=1}^{\log n} 2 \frac{n}{2^{j-3}}= 4n(1-\frac{1}{n})ビットとなります。
これを各ラウンドの計算を展開して(unrolling)最後の計算にまとめることで2n+2log n +1ビットの計算に代えることができます。
詳細は元論文[1]の3.1節を参照して下さい。
完全性の証明
証明者が正しい場合に検証者が必ず証明を受理することを示します。
n=1のときに成り立つことは明らかです。
n>1のときに完全性が成り立つことを示します。
記法としてH(\vec{a},\vec{a^{'}},\vec{b},\vec{b^{'}},c)をH(\vec{a},\vec{a^{'}},\vec{b},\vec{b^{'}},c)=\vec{g} _{[:n/2]}^{\vec{a}}\vec{g} _{[n/2:]}^{\vec{a^{'}}}\vec{h} _{[:n/2]}^{\vec{b}} \vec{h} _{[n/2:]}^{\vec{b}^{'}}u^{c}
と表すことにします。
するとこの関数は
\;\;\;H(\vec{a_1},\vec{a^{'}_1},\vec{b_1},\vec{b^{'}_1},c_1)\cdot H(\vec{a_2},\vec{a^{'}_2},\vec{b_2},\vec{b^{'}_2},c_2)
=(\vec{g} _{[:n/2]}^{\vec{a_1}}\vec{g} _{[n/2:]}^{\vec{a^{'}_1}}\vec{h}_{[:n/2]}^{\vec{b_1}}\vec{h}_{[n/2:]}^{\vec{b_1}^{'}}u^{c_1})\cdot (\vec{g}_{[:n/2]}^{\vec{a_2}}\vec{g}_{[n/2:]}^{\vec{a^{'}_2}}\vec{h}_{[:n/2]}^{\vec{b_2}}\vec{h} _{[n/2:]}^{\vec{b_2}^{'}}u^{c_2})
=H(\vec{a}_1+\vec{a}_2,\vec{a}^{'}_1+\vec{a}^{'}_2,\vec{b}_1+\vec{b}_2,\vec{b}^{'}_1+\vec{b}^{'}_2,c_1+c_2)
より、準同型という性質を持ちます。
上の証明プロトコルで証明者が正しい場合、P=\vec{g}^{\vec{a}}\vec{h}^{\vec{b}}u^{\braket{\vec{a},\vec{b}}}が成り立つので
\;\;\;P=\vec{g}^{\vec{a}}\vec{h}^{\vec{b}}u^{\braket{\vec{a},\vec{b}}}
=H(\vec{a}_{[:n/2]},\vec{a}_{[n/2:]},\vec{b}_{[:n/2]},\vec{b}_{[n/2:]},\braket{\vec{a},\vec{b}})
と表すことができます。また\vec{g}^{'\vec{a}'}\vec{h}^{'\vec{b}'}u^{\braket{\vec{a}',\vec{b}'}}を元のベクトルを用いて表すとHの準同型性より
\;\;\;\vec{g}^{'\vec{a}'}\vec{h}^{'\vec{b}'}u^{\braket{\vec{a}',\vec{b}'}}
=(\vec{g}_L^{x^{-1}} \vec{g}_R^{x})^{\vec{a}_L\cdot x+\vec{a}_R\cdot x^{-1}}(\vec{h}_L^{x^{-1}} \vec{h}_R^{x})^{\vec{b}_L\cdot x+\vec{b}_R\cdot x^{-1}}u^{\braket{\vec{a}',\vec{b}'}}
=\vec{g}_L^{\vec{a}_L + \vec{a}_R\cdot x^{-2}} \vec{g}_R^{\vec{a}_L\cdot x^2 +\vec{a}_R}\vec{h}_L^{\vec{b}_L+\vec{b}_R\cdot x^{-2}} \vec{h}_R^{\vec{b}_L\cdot x^2+\vec{b}_R}u^{\braket{\vec{a}',\vec{b}'}}
=H(\vec{a}_L + \vec{a}_R\cdot x^{-2},\vec{a}_L\cdot x^2 +\vec{a}_R,\vec{b}_L+\vec{b}_R\cdot x^{-2},\vec{b}_L\cdot x^2+\vec{b}_R,\braket{\vec{a}',\vec{b}'})
=H(0^{n/2},\vec{a}_L\cdot x^2 ,\vec{b}_R\cdot x^{2},0^{n/2},\braket{\vec{a}_L,\vec{b}_R})\cdot H(\vec{a}_L,\vec{a}_R,\vec{b}_L,\vec{b}_R,\braket{\vec{a},\vec{b}})
\cdot H(\vec{a}_R\cdot x^{-2},0^{n/2}, 0^{n/2},\vec{b}_R\cdot x^{-2},\braket{\vec{a}_R,\vec{b}_L})
=L^{x^2}\cdot P\cdot R^{x^{-2}}
という関係が成り立つので検証者は証明を受理します。
以上で完全性を示すことができました。
健全性の証明
以下Protocol 1の健全性を示します。
[1]ではエミュレータを用いて健全性(knowledge-soundness)を定義しています。
エミュレータとは対話証明において、証明したい文字列とその文字列を検証者に受理させることが可能な証明者の内部状態を用いて、証明者だけが持つ知識(と証明者と検証者のやりとり)を抽出することができるアルゴリズムのことです。
一方、エクストラクターは対話証明の証明者と検証者の全てのやりとりを受け取ると証明者だけが持つ知識を抽出することができるアルゴリズムです。
定義からエミュレータの方がエクストラクターよりも高い能力を持つことになります。(このあたりの理解が間違っていたら教えて下さい。)
エクストラクターやエミュレータによって証明から知識を抽出することができると、悪意のある(知識を持たない)証明者が検証者を納得させるような証明を送る確率は無視でき、健全性が成り立ちます。詳しくは[3]の記事を参照してください。
多項式回のやりとりで動作するエクストラクターを用いるとエミュレータを構成することができる([1]のTheorem 6)のでここではProtocol 1の多項式時間のエクストラクターの構成を示します。
Protocol 1のエクストラクターの構成は以下のように行います。どちらも離散対数問題の困難性を仮定します。
- ビット数に関する帰納法を用いたProtocol 2のエクストラクターの構成
- 1で構成したProtocol 2のエクストラクターを利用したProtocol 1の多項式時間のエクストラクターの構成
Protocol 2のエクストラクターの構成
Protocol 2で用いられる生成元を\vec{g}, \vec{h}, u、証明者が送ったコミットメントをPとします。
エクストラクターは証明者が送ったコミットメントから
内積の値を示したいベクトルのビット数に関する帰納法で示します。
(I) ビット数n=1のとき
n=1のときこのプロトコルでは証明者は検証者に(一次元の)ベクトルの値a, bそのものを送るので知識(a\cdot b = cを満たすa,b)を得ることができます。
(II) ビット数がn-1以下のエクストラクターの存在を仮定するとき
まずx_i \neq \pm x_jを満たす異なる4つのチャレンジx_i (i=1,\cdots 4 )に対するProtocol 2を4回実行することで検証者が納得するようなコミットメント
P_i = L^{x_i^2}PR^{x_i^{-2}}
を得ます。検証者が納得したという仮定から
L^{x^2}\cdot P\cdot R^{x^{-2}}=\vec{g}^{'\vec{a_i}'}\vec{h}^{'\vec{b_i}'}u^{\braket{{\vec{a_i}}',{\vec{b_i}}'}}
つまり
P_{i}=(\vec{g}_{[:n/2]}^{x_i^{-1}} \circ \vec{g}^{x_i}_{[n/2:]})^{\vec{a_i}'}\cdot(\vec{h}_{[:n/2]}^{x_i} \circ \vec{h} ^{x_{i}^{-1} } _{[n/2:]} )^{\vec{b_i}'} u^{\braket{ \vec{a_i}',\vec{b_i}'} }\;\;\; (3)
が成り立ちます。
帰納法の仮定からベクトルのビット数がビット数n-1以下のときにはエクストラクターが存在するので、これらのコミットメントから(3)を満たすベクトルの組(\vec {a'_i}, \vec {b'_i})\;(i=1,\cdots 4)を得ることができます。
これらのうち3つだけ\vec {a_i}', \vec {b_i}', x_i (i=1,\cdots 3)を用いて
1.(\sum_{i=1}^{3}\nu _i \cdot x_i ^2,\sum_{i=1}^{3}\nu _i , \sum_{i=1}^{3}\nu _i \cdot x_i ^{-2} ) = (1,0,0) \;\;\; (4)を満たす\nu _iを三元一次方程式を解くことで求める
2.\vec{a_L} = [\sum_{i=1}^{3} x_i ^{-1}\cdot \nu_i\cdot \vec {a'_i},\sum_{i=1}^{3} x_i \cdot \nu_i \cdot \vec {a_i}']
\vec{b_L} = [\sum_{i=1}^{3} x_i \cdot \nu _i\cdot \vec {b_i}',\sum_{i=1}^{3} x_i^{-1} \cdot \nu _i \cdot \vec{b_i}'] c_L = \sum_{i=1}^{3} \nu _i\cdot \braket{\vec{a_i}',\vec{b_i}'}を計算する([\vec{v_1}, \vec{v_2}]は\vec{v_1}, \vec{v_2}を並べたベクトルを表す)
の2ステップで\vec {a_L}, \vec {b_L},c_Lを得ると
\;\;\;\vec{g}^{\vec{a_L}}\vec{h}^{\vec{b_L}}u^{c_L} = \prod_{i=1}^{3}(\vec{g}_{[:n/2]}^{\nu_{i} x_{i}^{-1}}\circ \vec{g}_{[n/2:]}^{\nu_{i} x_{i}})^{\vec{a_i}'}(\vec{h}_{[:n/2]}^{\nu_i x_i} \circ \vec{h}_{[n/2:]}^{\nu_i x_i^{-1}})^{\vec{a_i}'}\vec{h}^{\vec{b_L}} u^{\nu_{i}\braket{\vec {a_i}',\vec {b_i}'} }= \prod_{i=1}^{3} P_i ^{\nu_i}
= L^{\sum_{i=1}^{3} \nu_i \cdot x_i^2} \cdot P^{\sum_{i=1}^{3}\nu_i } \cdot R^{\sum_{i=1}^{3}\nu _i \cdot x_i ^{-2}}
より(4)式から
\vec{g}^{\vec{a_L}}\vec{h}^{\vec{b_L}}u^{c_L} = L
が成り立ちます。同様に(4)の代わりに(\sum_{i=1}^{3}\nu _i \cdot x_i ^2,\sum_{i=1}^{3}\nu _i , \sum_{i=1}^{3}\nu _i \cdot x_i ^{-2} ) = (0,1,0),(0,0,1)としてステップ1,2を繰り返すことでそれぞれ
\vec{g}^{\vec{a_P}}\vec{h}^{\vec{b_P}}u^{c_P} = P, \vec{g}^{\vec{a_R}}\vec{h}^{\vec{b_R}}u^{c_R} = R
を満たす\vec {a_P}, \vec {b_P},c_P, \vec {a_R}, \vec {b_R},c_Rを得ることができます。
これらの値を用いて関係式(3)を書き直すとx_i \in \{x_1, x_2, x_3, x_4 \}と対応する\vec {a'}, \vec {b'}に対して
\text{(左辺)} =L^{x^2}PR^{x^{-2}} = \vec{g}^{\vec{a_L}\cdot x^{2} + \vec{a_P} + \vec{a_R} \cdot x^{-2}}\vec{h}^{\vec{a_L}\cdot x^{2} + \vec{b_P} + \vec{b_R} \cdot x^{-2}}u^{c_L\cdot x^{2}+c_P + c_R\cdot x^{-2}}
\text{(右辺)} = (\vec{g}_{[:n/2]}^{x^{-1}} \circ \vec{g}^{x}_{[n/2:]})^{\vec{a}'}\cdot(\vec{h}_{[:n/2]}^{x} \circ \vec{h} ^{x_{i}^{-1} } _{[n/2:]} )^{\vec{b}'} u^{\braket{ \vec{a}',\vec{b}'} } =\vec{g}_{[:n/2]}^{a'\cdot x^{-1}} \vec{g}^{a' \cdot x}_{[n/2:]}\cdot \vec{h}_{[:n/2]}^{\vec{b}' \cdot x} \circ \vec{h} ^{\vec{b}'\cdot x^{-1} } _{[n/2:]} u^{\braket{ \vec{a}',\vec{b}'} }
となるので
\vec{g}^{\vec{a_L}\cdot x^{2} + \vec{a_P} + \vec{a_R} \cdot x^{-2}}\vec{h}^{\vec{a_L}\cdot x^{2} + \vec{b_P} + \vec{b_R} \cdot x^{-2}}u^{c_L\cdot x^{2}+c_P + c_R\cdot x^{-2}} = \vec{g}_{[:n/2]}^{a'\cdot x^{-1}} \vec{g}^{a' \cdot x}_{[n/2:]}\cdot \vec{h}_{[:n/2]}^{\vec{b}' \cdot x} \circ \vec{h} ^{\vec{b}'\cdot x^{-1} } _{[n/2:]} u^{\braket{ \vec{a}',\vec{b}'} } \;\;\;(5)
が成り立ちます。
すると離散対数問題の困難性の元では無視できる確率を除いて
\vec{a}' \cdot x^{-1} = \vec{a}_{L, [:n/2]}\cdot x^{2} + \vec{a}_{P, [:n/2]} + \vec{a}_{R,[:n/2]}\cdot x^{-2}\;\;\;(6)
\vec{a}' \cdot x = \vec{a}_{L, [n/2:]}\cdot x^{2} + \vec{a}_{P, [n/2:]} + \vec{a}_{R,[n/2:]}\cdot x^{-2}\;\;\;(7)
\vec{b}' \cdot x = \vec{b}_{L, [:n/2]}\cdot x^{2} + \vec{b}_{P, [:n/2]} + \vec{b}_{R,[:n/2]}\cdot x^{-2}\;\;\;(8)
\vec{b}' \cdot x^{-1} = \vec{b}_{L, [n/2:]}\cdot x^{2} + \vec{b}_{P, [n/2:]} + \vec{b}_{R,[n/2:]}\cdot x^{-2}\;\;\;(9)
\braket{\vec{a}', \vec{b}'} = c_{L}\cdot x^{2} + c_{P} + c_{R}\cdot x^{-2}\;\;\;(10)
が成り立ちます。
(\because(5)を変形すると
\vec{g}_{[:n/2]}^{\vec{a}_{L, [:n/2]}\cdot x^{2} + \vec{a}_{P, [:n/2]}+ \vec{a}_{R,[:n/2]}\cdot x^{-2} -\vec{a}' \cdot x^{-1} }\vec{g}_{[n/2 :]}^{\vec{a}_{L, [n/2:]}\cdot x^{2} + \vec{a}_{P, [n/2:]} + \vec{a}_{R,[n/2:]}\cdot x^{-2}- \vec{a}' \cdot x}
\vec{h}_{[:n/2]}^{\vec{b}_{L, [:n/2]}\cdot x^{2} + \vec{b}_{P, [:n/2]} + \vec{b}_{R,[:n/2]}\cdot x^{-2} - \vec{b}' \cdot x}\vec{h}_{[n/2:]}^{\vec{b}_{L, [n/2:]}\cdot x^{2} + \vec{b}_{P, [n/2:]} + \vec{b}_{R,[n/2:]}\cdot x^{-2} - \vec{b}' \cdot x^{-1}}u^{c_{L}\cdot x^{2} + c_{P} + c_{R}\cdot x^{-2} - \braket{\vec{a}', \vec{b}'}} = 1
となりますが、例えば(6)(7)(8)(9)(10)のうち一つでも成り立たないとすると\vec{g}_{[:n/2]}^{\vec{a}_1}\vec{g}_{[n/2:]}^{\vec{a}_2}\vec{h}_{[:n/2]}^{\vec{b}_1}\vec{h}_{[n/2:]}^{\vec{b}_2}u^c = 1を満たす、全てが0ではない\vec{a}_1, \vec{a}_2, \vec{b}_1, \vec{b}_2, cが得られてしまい、困難なはずの離散対数問題を解けてしまいます。)
これらの式から
(6)\times x - (7)\times x^{-1}より\vec{a}_{L,[:n/2]}\cdot x^3 + (\vec{a}_{P, [:n/2]}-\vec{a}_{L,[n/2:]})\cdot x + (\vec{a}_{R,[:n/2]}-\vec{a}_{P,[n/2:]})\cdot x^{-1}- \vec{a}_{R,[n/2:]}\cdot x^{-3} = 0 \;\;\;(11)
-(8)\times x^{-1} + (9)\times xより\vec{b}_{L,[n/2:]}\cdot x^3 + (\vec{b}_{P, [n/2:]}-\vec{b}_{L,[:n/2]})\cdot x + (\vec{b}_{R,[n/2:]}-\vec{b}_{P,[:n/2]})\cdot x^{-1}- \vec{b}_{R,[:n/2]}\cdot x^{-3} = 0\;\;\; (12)
がx_i \neq \pm x_jを満たす異なる4つのチャレンジx_i (i=1,\cdots 4 )に対して成り立つことから、
\vec{a}_{L,[:n/2]} = \vec{a}_{R,[n/2:]} = \vec{b}_{R,[:n/2]} = \vec{b}_{L,[n/2:]}
\vec{a}_{P, [:n/2]}=\vec{a}_{L,[n/2:]},\; \vec{a}_{R,[:n/2]}=\vec{a}_{P,[n/2:]}
\vec{b}_{P, [:n/2]}=\vec{b}_{L,[n/2:]},\; \vec{b}_{R,[n/2:]}=\vec{b}_{P,[:n/2]}
が成り立ちます。
(\because (11),(12)の両辺にx^3をかけてx^2に関する三次方程式と見るとこの方程式の根は最大で3つしか存在しないことから従います。ここでx_i \neq \pm x_jであることが効いてきます。)
さらに\vec{a}' = \vec{a}_R x^{-1} + \vec{a}_L xに注意すると(6)\times x + (7)\times x^{-1}から\vec{a}' = \vec{a}_{P, [:n/2]} x + \vec{a}_{P, [n/2:]} x^{-1}
同様に(8),(9)から\vec{b}' = \vec{b}_{P, [:n/2]} x^{-1} + \vec{b}_{P, [n/2:]} xが成り立つので(10)から
\;\;\;c_{L}\cdot x^{2} + c_{P} + c_{R}\cdot x^{-2}
= \braket{\vec{a}_{P, [:n/2]} x + \vec{a}_{P, [n/2:]} x^{-1}, \vec{b}_{P, [:n/2]} x^{-1} + \vec{b}_{P, [n/2:]} x}
= \braket{\vec{a}_{P, [:n/2]}, \vec{b}_{P, [n/2:]}}x^2 + \braket{\vec{a}_{P, [:n/2]}, \vec{b}_{P, [:n/2]}} +\braket{\vec{a}_{P, [n/2:]}, \vec{b}_{P, [n/2:]}}+\braket{\vec{a}_{P, [n/2:]}, \vec{b}_{P, [:n/2]}}\cdot x^{-2}
= \braket{\vec{a}_{P, [:n/2]}, \vec{b}_{P, [n/2:]}}x^2 + \braket{\vec{a}_{P}, \vec{b}_{P}}+\braket{\vec{a}_{P, [n/2:]}, \vec{b}_{P, [:n/2]}}\cdot x^{-2}
これがx_i \neq \pm x_jを満たす異なる4つのチャレンジx_i (i=1,\cdots 4 )に対して成りたつことから上と同様の理由で
\braket{\vec{a}_P, \vec{b}_P} = c_Pが成り立ちます。
従ってエクストラクターは\braket{\vec{a}, \vec{b}} = c_Pを満たすベクトルの組(\vec{a},\vec{b})として(\vec{a}_P, \vec{b}_P)を得ることできました。
このProtocol 2のエクストラクターは一度の証明に4回のやりとりを行い、その回数は入力長の対数で抑えられるので合計のやりとりの回数はO(4^{\log n}) = n^2となり、
やりとりの数も入力長の多項式で抑えることができます。
Protocol 1の多項式時間のエクストラクターの構成
Protocol 1で用いられる公開された生成元を\vec{g},\vec{h},u, コミットメントと内積の値をP,cとします。
Protocol 1を2回実行することで異なるチャレンジx, x'に対するProtocol 1の検証者を納得させるような証明を得たとします。
するとそれぞれの証明からProtocol 2のエクストラクターを用いることでP\cdot u^{x\cdot x} = \vec{g}^{\vec{a}}\vec{h}^{\vec{b}}u^{x\cdot \braket{\vec{a},\vec{b}}}、P\cdot u^{x\cdot x'} = \vec{g}^{\vec{a}}\vec{h}^{\vec{b}}u^{x'\cdot \braket{\vec{a}',\vec{b}'}}を満たす知識(\vec{a},\vec{b}),(\vec{a}',\vec{b}')を抽出できます。
この式の辺々を割り算すると
u^{(x-x')c}=\vec{g}^{\vec{a}-\vec{a}'}\vec{h}^{\vec{b}-\vec{b}'}u^{x\cdot \braket{\vec{a},\vec{b}}-x'\cdot \braket{\vec{a}',\vec{b}'}}
離散対数問題の困難性を仮定すると、Protol 2のエクストラクターの構成のときと同じ理由で
\vec{a}=\vec{a}', \vec{b}=\vec{b}', (x-x')c = x\cdot \braket{\vec{a},\vec{b}}-x'\cdot \braket{\vec{a}',\vec{b}'}
が成り立つのでc = \braket{\vec{a},\vec{b}}を得ることができます。
Protocol2エクストラクターのやりとりの回数が多項式で抑えられることから、Protocol1のエクストラクターのやりとりの回数も多項式で抑えることができます。
Range Proofへの応用
この内積アーギュメントを利用すると「ある値が一定の区間に入っていること」を示すrange proofのプロトコルを構成することができます。
[2]に日本語でわかり易く解説されているのでこちらを参照して下さい。
理解不足の点
- 論文の健全性について理解しきれていません。エミュレータやエクストラクターの理解が曖昧です。分岐補題(Forking lemma)とも関連があるようですがこの点も理解できていません。
- このプロトコルはSNARKに応用される際にはFiat-Shamir変換によって対話型から非対話に変換されているそうだがそもそもFiat-Shamir変換を理解していません。SNARKを応用したPCDの健全性の理解のためにはこのあたりの理解も必要だと思われます。
参考文献
[1]Bulletproofs: Short Proofs for Confidential Transactions and More
[2]Bulletproofsを利用したrange proofの仕組み - Develop with pleasure!
[3]知識抽出機(Knowledge Extractor)とは?知識抽出可能性と健全性の関係 | HashPort技術ブログ