計算・通信量を効率化する拡張紛失通信プロトコル SoftSpokenOT の紹介

はじめに

この記事では 計算・通信量を効率化する拡張紛失通信プロトコル SoftSpokenOT の論文¹を紹介します。

紛失通信プロトコルの概要については²の記事を参照してください。拡張紛失通信プロトコル(OT extension)とは、紛失通信プロトコルを内部的に利用して、単純に並列で紛失通信プロトコルを実行する場合よりも多くの紛失通信を実行するプロトコルです。これは例えるならば公開鍵暗号において、対称鍵暗号の鍵を暗号化して、その対称鍵暗号鍵自体を使って実際のデータを暗号化するような仕組みと似ています。代表的なものとしては³⁴などがあります。

SoftSpokenOTは ECDSAの3ラウンドt-of-n 閾値署名アルゴリズムの解説 ⁵記事で拡張紛失通信プロトコルの基礎として使われています。また、この論文中では以前の閾値ECDSAの論文⁶中で使われている拡張紛失通信プロトコルであるKOSプロトコルの脆弱性についても指摘しています。この脆弱性は⁶の実装に影響を与える可能性があり、実用上も重要なものです。

SoftSpokenOTは³⁴における計算量と通信量を削減し、さらにトレードオフとして一方をさらに削減する方法を提案しています。

プロトコルの解説

以下のように、本プロトコルは様々な種類の紛失通信プロトコルを利用することで成り立っている。

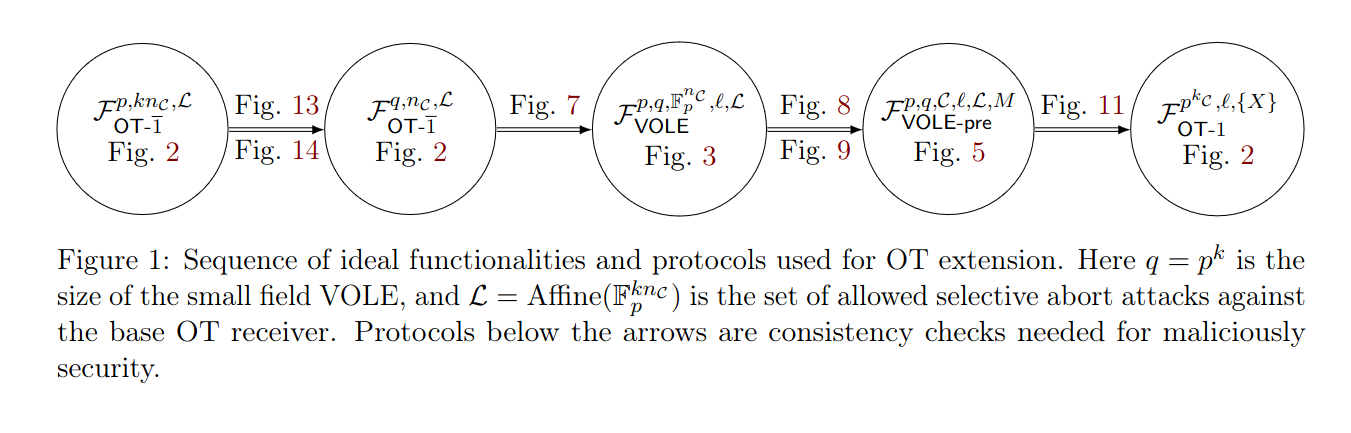
具体的には⁴などを参照してほしいが、紛失通信プロトコルの中で別の紛失通信プロトコルを実行するということが行われている。
上図矢印上段は受動的な攻撃者に対する「弱い」プロコトルに必要なものであり、矢印下段は能動的な攻撃者に対する「強い」プロトコルに追加で必要なアルゴリズムである。

事前知識

(N, k)-OT

(N, k)-OTとは、N個のうち受信者が選択したk要素を取得し、N-k要素についての知識を得ることができないようなOTである。

(N, N-1)-OTの実現

この論文では (N, N-1)-OTを (2, 1)-OTから実現する方法については触れられていない。⁷に詳細が記載されている。

(N, N-1)-OTを利用した計算量の少ない(N, N-1)-OTの実現

¹の 6. Base OTs Figure 13で触れられている。これも他の論文の成果⁸を参照している。

(N, N-1)-OTを利用したVOLEの実現

VOLEについて解説した3章の、3.1 For Small Fieldsで解説されている。
具体的には F_{\text{VOLE}}^{p,q,\mathbb{F}_p,l,L}を実装していることを確認する。
以下の図にあるように、Fのq(=p^k)要素のうちq-1要素がP_R（受信者）に紛失通信を1インスタンスだけ使って送信され、F全体がP_S(送信者)に与えられる。
kはセキュリティパラメータ\lambdaを調整するためのパラメータであり、本来\lambdaビット分の紛失通信をしていた部分を、\lambda/kビットに圧縮しようとすると、計算コストが 2^k / k倍になる。

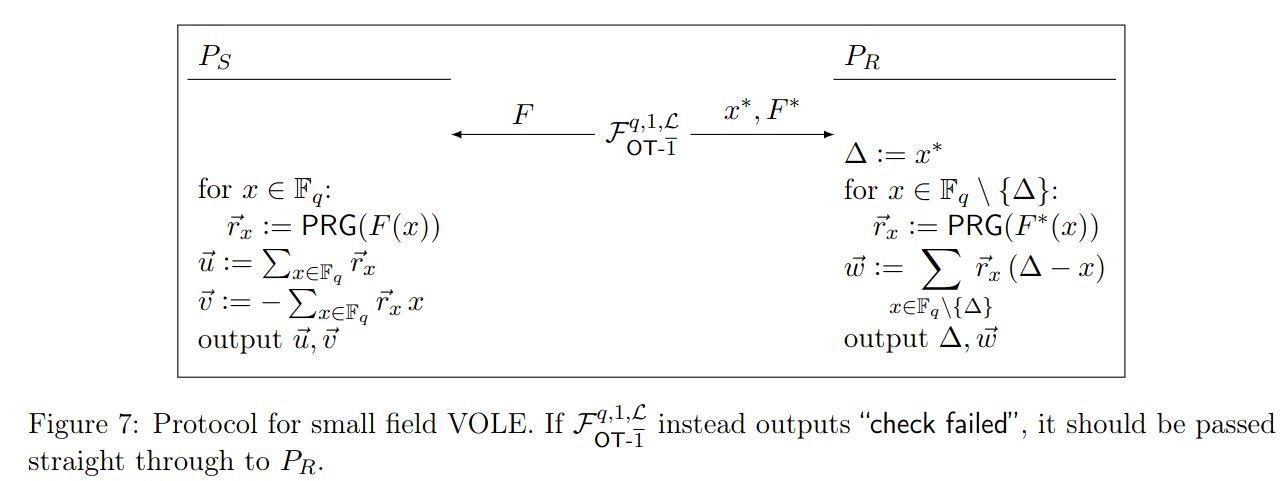
ここで送信されなかった要素のインデックス番号が \Delta = x^*である。(q,q-1)-OTで生成される乱数はここでは関数(punctured Pseudo Random Function)として定義されており、P_RもP_Sも同じ関数Fにアクセスできるが、P_Rは一点\DeltaにおけるF(\Delta)にはアクセスできず、この定義域を欠いた関数がF^*である。
VOLEにおいて結果的に出力される変数(P_Sの\vec{u}, \vec{v}、P_Rの\Delta, \vec{w})の値は式「\vec{w} = \vec{u} G_C \text{diag}(\Delta) + \vec{v}」を満たしている必要がある。

ここで G_C \in \mathbb{F}_p^{k_C\times n_C}は線形符号Cの生成行列であるが、定義からG_{\mathbb{F}_p^n} = \mathbf{1}_nでありG_{\mathbb{F}_p} = 1かつn_{\mathbb{F}_p} = 1であるから、\Deltaの次元は1であり結局G_{\mathbb{F}_p} \text{diag}(\Delta) = \Deltaである。

\vec{u}, \vec{v}, \vec{w}, \Delta, Cが上記の関係を満たすことを示す。

\vec{w} = \sum_{x \in \mathbb{F}_q \backslash \{\Delta\}} \vec{r_x} (\Delta - x) = \sum_{x \in \mathbb{F}_q } \vec{r_x} (\Delta - x) = \sum_{x \in \mathbb{F}_q } \vec{r_x}\Delta - \sum_{x \in \mathbb{F}_q } \vec{r_x} x = \vec{u} \Delta + \vec{v} によって満たされる。

VOLEを利用した部分空間VOLEの実現

VOLEについて解説した3章の、3.2 For Subspaces で解説されている。
具体的には F_{\text{VOLE-pre}}^{p,q,C,l,L,M}を実現していることを確認する。機能 F_{\text{VOLE-pre}}は 受動的な攻撃者を仮定する場合にはF_{\text{VOLE}}と変わらない。

能動的な攻撃者を仮定する場合には 以下Figure 9のような一貫性チェックのプロトコルが追加される。

部分空間VOLEを利用したバッチ(N, 1)-OTの実現

5章 OT Extensionにて解説されている。

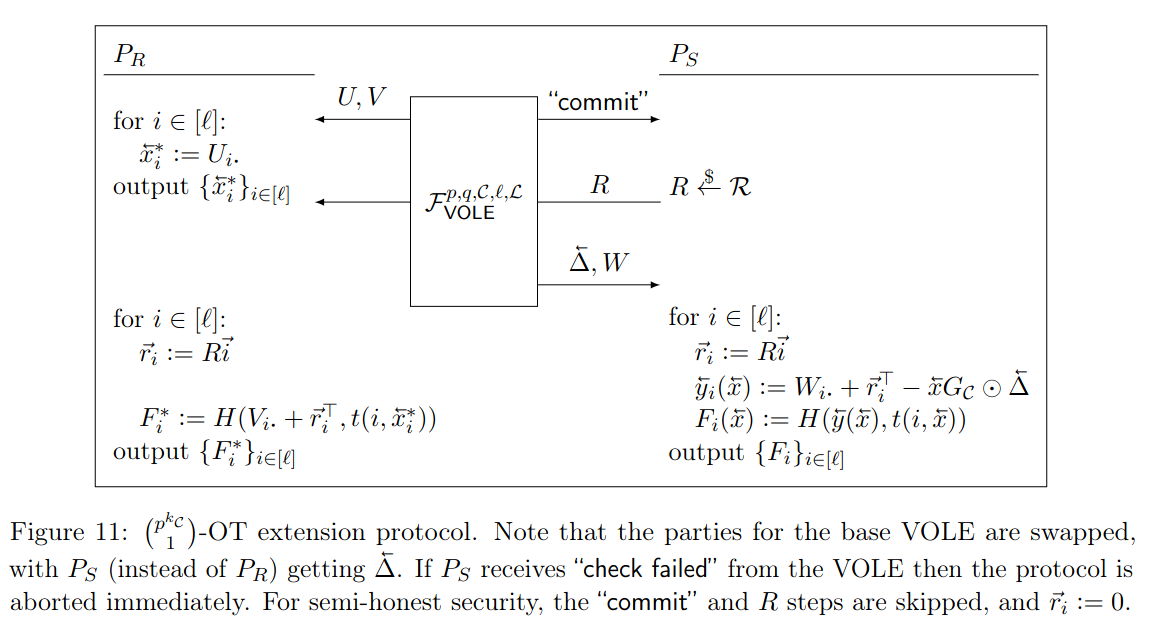
これが F_{\text{OT-1}}^{N, l, L}を実現することを確認する。
これはl個の1-of-N紛失通信を並列に実行しようとしている。x_i^*はi番目の紛失通信において受信者P_Rが選択するインデクスである。ランダムな関数F_i(i = 1...N)の値域が送信者が送ろうとする値の候補になる。

F_{\text{VOLE}}を実行することで、P_RはランダムなU, Vを入手し、P_Sは\Delta, Wを入手する。これらの変数はW = \Delta U + Vを満たす。Rは一貫性チェックのために使われる行列である。

Uがインデックスとして扱われることに注意すると、「P_Rのみが知っているランダムな値 x_i^*を入力したときだけ、P_Rの持っている情報から復元できる値になるような関数F_i」をP_Sが作ることができる。

P_Rのみが知っている情報はUだけではなくVもあるので、その値を使って入力をマスクできるおかげで、このようなことが可能になっている。
また、一方でWの値はP_Sのみが知っているので、Wによってマスクされた他の値をP_Rが入手することはできない。

結局、このプロトコルが完了すると P_Rはランダムな値をl個受け取り、P_Sはランダムな値を出力する関数をl個受け取ることになる。

まとめ

乱数列を扱うときは、乱数列そのものではなく乱数を生成する関数として扱うことができ、かつ、乱数列を紛失通信で処理できればその乱数列を共通鍵暗号の鍵として扱うことができるようにもなる、といった前提が省略されているのでややわかりにくかったです。

参考文献