はじめに
本稿では暗号通貨Monero(モネロ, XMR)のアップグレードにて導入される予定のフルチェーンメンバーシップ証明(Full Chain Membership Proof; FCMP)プロトコルや、ビットコインUTXOを使ったシビル攻撃耐性のある匿名ユーザー参加型プロトコル1などの基礎になっている、ゼロ知識集合メンバーシップ証明プロトコルである楕円曲線木(Curve Trees)2について解説します。
ゼロ知識集合メンバーシップ証明とは
集合Sのダイジェストが与えられたとします。例えば、マークル木のルートハッシュなどが想定できます。マークル木の葉ノードが集合Sの各要素だとすると、ルートハッシュで指定される葉ノードの集合Sの中に、ある要素が入っていると示すことができます。すなわち、マークル木の認証パスを並べて、証明したい要素の葉ノードから順番にハッシュすることによって、ある葉ノードが集合Sの中に含まれることを証明できます。
これを、葉ノードを検証者に公開せずに行うのがゼロ知識集合メンバーシップ証明です。zkSNARKを用いた例として、トルネードキャッシュ(Tornado Cash)34でも利用されています。
zcashやトルネードキャッシュで採用されているzkSNRKではトラステッドセットアップや楕円曲線ペアリングなどの暗号学的仮定が必要ですが、ここで紹介する楕円曲線木はランダムオラクル仮定と離散対数問題の困難性のみを暗号学的仮定としていることに特徴があります。
前提知識
ピダーセンコミットメントとゼロ知識証明
ピダーセンコミットメントは、コミットしたいベクトル\vec{v}と楕円曲線上の点である公開生成元\vec{G}, Hに対して、コミットしたい人が生成した乱数rを使って C = \langle \vec{v}, \vec{G} \rangle + [r]Hで計算されます。
コミットメントをオープンするには、単に\vec{v}, rを公開し、検証者が同じように計算します。
もし\vec{v}, rを公開せずに、このコミットメントの原像を知っていることを証明したい場合、Bulletproofs5を使うことによって、証明できます。
BulletproofsによるR1CS制約のゼロ知識証明
以前紹介したBulletproofsの記事5では、単純なベクトルの内積のゼロ知識証明について書きました。これは、証明したいある複数の値の関係において、それらが「内積計算の結果になる」という制約を表現しているものであったといえます。
今回のBulletproofsは、証明したいある複数の値の関係において、ベクトルの内積という制約だけではなく、R1CSという足し算と掛け算を使った制約(すなわち、コンピュータにおける任意の表現が可能な制約)に一般化して、ゼロ知識証明を行うものになります。ただ、これはより一般的なフォーマットであるR1CSの方が扱いやすいというだけであり、本質的にはやっていることは内積の制約を証明することと変わりません。R1CSの制約を内積の制約に変換する方法については6を参照してください。
なぜBulletproofsだけでは駄目なのか
上記で説明した通り、R1CSという足し算と掛け算を使った制約によって、直接「ゼロ知識集合メンバーシップ証明」を記述することもできます。
すなわち、(1)ゼロ知識で証明したい値(秘匿したい集合の要素と、そのインデックス)を非公開入力として、集合Sのダイジェストとそこに含まれているはずの要素自体を公開入力とするような回路を考えて、(2)その回路をR1CSで表現した後、(3)Bulletproofs上で内積計算の制約として表現し直しさえすれば、ゼロ知識証明が実現できることになります。
これが正しければBulletproofsだけですべてが完結し、楕円曲線木が登場する余地はないように思われます。もしも上記(1)で考えた回路が単純なものであり、(2)のR1CS表現に変換する際にオーバーヘッドが存在しなければ楕円曲線木は不要なのですが、実際には(1)の回路をナイーブに実装すると(2)の変換の際にR1CSの式の制約数がとても大きくなり、したがって結果的に生成されるゼロ知識証明のサイズや計算時間も現実的なものではなくなってしまいます。
そこで、(1)の回路を直接作るかわりに、楕円曲線木というデータ構造を導入して(2)の変換が低コストで実行できるようにしているのがこの論文です。
楕円曲線木の概要
以前楕円曲線ペア7を本ブログでも紹介しましたが、楕円曲線木においてはこの楕円曲線ペアを使ったマークル木のようなデータ構造を作ります。マークル木のレイヤー数(階層の数)がD層であり、一つのノードが持つ子ノードの数をl個とします。木のルート(根)を一番上に置いて0番目の層とすると、上から0\le k \lt D-1番目の階層にあるノードは l^k個の要素になり、それぞれの要素がl個の子ノードを持ちます。そしてD-1番目の階層にあるノードは l^{D-1}個であり、それぞれが一つずつ子ノード(D番目の層の葉ノード)を持ちます。楕円曲線ペアは二種類の曲線を持ち、それぞれの点の集合を E_{(evn)}, E_{(odd)}とすると、上記の木の偶数番目の層のノードは E_{(evn)}に属する点を持ち、奇数番目の層のノードは E_{(odd)}に属する点を持てるようにしておきます。
第k層の楕円曲線上の点のx座標からなるベクトルとy座標からなるベクトルを使って作成したコミットメントが、第k-1層のノード(根を上に置いたとき、k層の一つ上の層)の点になるという関係を持つように、葉から根まで計算していきます。
このようにして構築された木を検証者が共有しているとします。証明者は一つ上の層を計算する部分でランダム化因子を混ぜ込み、l個の子のうち、どの子ノードを保有しているのかを隠しつつ、あらかじめ共有された木の根と一致するようなパスを効率的に証明として作成することができます。
この証明では内部的にBulletproofs5が使われています。
以下の画像は楕円曲線木の具体例と概略を示しています。
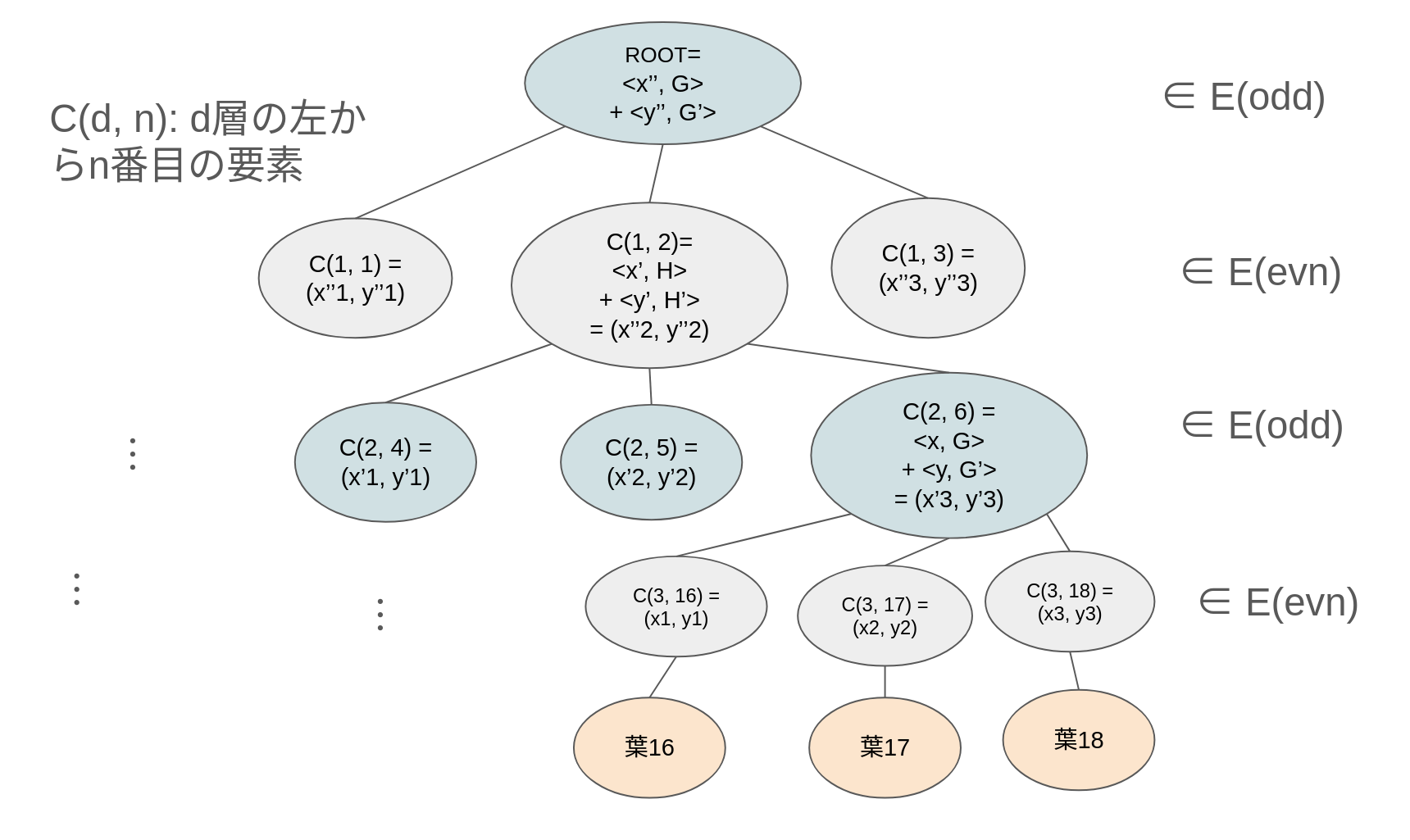
ここでは深さD=4であり、中間ノードの持つ子の数l=3としています。
葉ノードはそのまま、E_{\text{(evn)}}の楕円曲線上の点の値として扱います。
中間ノードを計算するには、子ノードそれぞれのx座標ベクトル、y座標ベクトルを使ってC = \langle \vec{x}, \vec{G_{\text{(\_)}}^{x}}\rangle + \langle \vec{y}, \vec{G_{\text{(\_)}}^{y}}\rangle \in E_{\text{other(\_)}}のように計算します。ここで \vec{G_{\text{(\_)}}^{x}}, \vec{G_{\text{(\_)}}^{y}}は公開されたランダムな生成元のベクトルで、子ノードの点の楕円曲線の種類と一致します。また、E_{\text{other(\_)}}は子ノードの点の楕円曲線とは、異なる楕円曲線の種類になります(子がevnならodd, oddならevn)。
これを木の全体で下の葉から繰り返し適用し、上のルートノードまで計算します。
一番上のROOTが集合のダイジェストに相当し、下の葉が集合の要素に該当しています。なおこの図では27要素の集合の一部分(16, 17, 18のみ)が計算されていますが、木全体の値が少なくとも一度は計算される必要があります(ただし、証明を作成する際には図のように一部分だけを計算すればよく、残りは再計算不要です)。
楕円曲線木の各層における証明
楕円曲線木を上記のように構成し、中間ノードと子ノードを準備し終えたとします。下の層の特定のノードXが上の層のノードにコミットされていることを、Xを明かすことなく示したい場合、非公開入力(i, r, \delta, \vec{x}, \vec{y})に対して以下の2つの制約(a)(b)を証明することになります。ここでiは選択した子ノードの番号、r, \deltaは証明者が選ぶランダムな数値、\vec{x}, \vec{y}は子ノードの点のx座標、y座標をそれぞれ並べてベクトルにしたものです。
また、以下のC, \hat{C}は公開入力になります。
(a) 親ノードをオープンする制約
これは C = \langle \vec{x}, \vec{G_{\text{(\_)}}^{x}}\rangle + \langle \vec{y}, \vec{G_{\text{(\_)}}^{y}}\rangle + [r] H_{\text{(\_)}} \in E_{\text{(\_)}} で表現できます。この制約は、楕円曲線木の中間ノードを計算したときの点と見比べると、ピダーセンコミットメントそのものになっていることがわかります。よって、直接Bulletproofsで証明することができ、楕円曲線木を使わない場合よりも効率的になります。
(b) i番目の子ノードをランダム化する制約
\hat{C} = (x_i, y_i) + [\delta] H_{\text{other(\_)}} \in E_{\text{other(\_)}} で表現できます。
残念ながら、この制約はピダーセンコミットメントになっていたりはしないので、R1CSの制約条件として書き下す必要があります。書き下す方法については論文の補遺Bに書かれています。
ピダーセンコミットメントであるためには、上述の通り公開された点Pとその係数を足し合わせるような式になっている必要がありますが、ここで (x_i, y_i)は公開できない点であるため、ピダーセンコミットメントの形式としては扱えません。
層ごとの制約の定義
上記の制約を満たす変数が存在する関係を\mathcal{R}^{\text{single-level}, E_{\text{(\_)}}}として定義しておきます。
層をまたいだ証明
上記の層ごとの制約が、各層においてすべて成立するような、以下の制約を考えます。この制約を満たす値を知っているということを、Bulletproofsによって証明できればよいことになります。
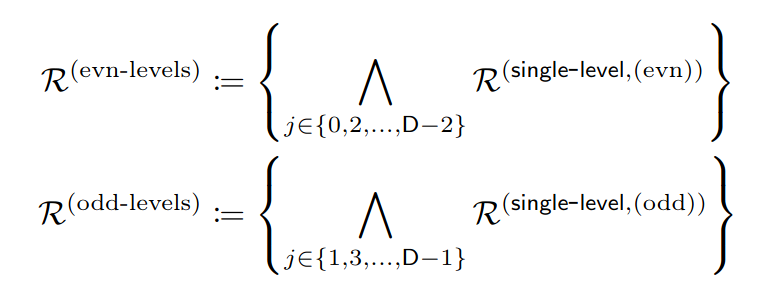
なお子ノードをオープンする制約(b)については、論文中に解説されているアルゴリズムでは公開入力としての値が入っていない(=x(evn), x(odd)の定義から抜けている)ように見えますが、これは計算の結果得られるノードの値は上下の層において一致するためです。すなわち、上の層の制約(b)の計算結果Cが、下の層の制約(a)の計算結果\hat{C}に一致しています。この一致によって、ランダム化した後であっても上下の層が接続されている条件を維持することができます。
大まかに言って(a)の制約は楕円曲線木の中間ノードの子ノードが多くなるとコストが高くなり、(b)の制約は楕円曲線木の高さが高くなるほどコストが高くなります。(b)の制約は、ピダーセンコミットメントとして表現できない分(a)と比べて圧倒的にコストが高いので、できるだけ中間ノードの幅を広くとるようにすることで、最適な計算コストが導出されます。
以下の表からも分かるように(集合要素数にもよりますが)、木の高さD=2,4などに対して中間ノードの子ノード数 l = 256, 1024 など、高さよりも幅が大きい歪な形の木になっています。
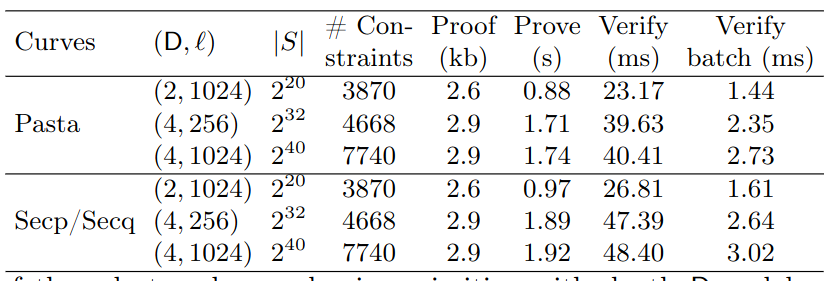
SelRerand(Select-and-Rerandomize; 選択と再ランダム化)のアルゴリズムとして掲載されている最終的なもののうち、証明と検証部分については以下のとおりです。
証明
この証明アルゴリズムでは、制約(a)(b)において、共通の乱数を使っていることがわかります。
また、E_{(evn)}, E_{(odd)}それぞれの楕円曲線における関係が独立に証明されています。これらを混ぜ合わせないことによって効率化を図っていることが確認できます。

検証
こちらでもE_{(evn)}, E_{(odd)}それぞれの楕円曲線における関係が独立に検証されています。

感想
この論文では2.1.3で楕円曲線サイクルについて「攻撃手法が知られていない」ことから仮定に含めていないようですが、厳密には安全な楕円曲線サイクルが成立するという仮定は離散対数問題とランダムオラクル仮定のいずれにも帰着できないのではないかと思います。
最終的にR1CSとBulletproofsを使うという流れは変わらないので、複雑さを減らすための計算上のトリックとして解釈するのがいいかと思いました。
参考文献
-
Anonymous usage tokens from curve trees or autct https://delvingbitcoin.org/t/anonymous-usage-tokens-from-curve-trees-or-autct/862 ↩
-
Curve Trees: Practical and Transparent Zero-Knowledge Accumulators https://eprint.iacr.org/2022/756.pdf ↩
-
Tornado cash. Non-custodial private transactions on Ethereum. https://github.com/tornadocash/tornado-core ↩
-
Tornado Cash https://git.tornado.ws/tornadocash/ ↩
-
内積アーギュメント Bulletproofsについて https://tech.hashport.io/3723/ ↩ ↩ ↩
-
Module bulletproofs::notes::r1cs_proof | Constraint system notation https://doc-internal.dalek.rs/bulletproofs/notes/r1cs_proof/index.html#constraint-system-notation ↩
-
第三者を信頼せずに段階的検証可能計算(IVC)を実現するHaloの解説 | 再帰的(S)NARKで使われる楕円曲線ペア https://tech.hashport.io/3778/ ↩


