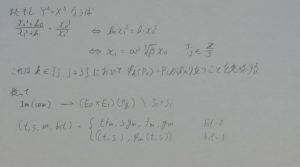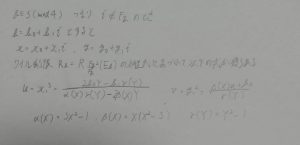本稿では、この論文を扱います。
https://eprint.iacr.org/2020/010.pdf
この記事で紹介する内容
楕円曲線暗号の多くのプロトコル(ペアリングなど)で用いられる標数pの有限体F_q上のj-不変量が0の楕円曲線上の点を圧縮する「二重点圧縮」の簡単な式を得る方法。
この際用いられる楕円曲線はE_b: y^2 = x^3 + bで表される。ここでb ∈ F^{*}_qである。
そもそもbitcoinで使われているsecp256k1の圧縮公開鍵のサイズを見れば分かるように本来楕円曲線上の点Pのx座標だけを保存しておく(圧縮)ことで本来の楕円曲線上の点Pを回復(復元)することができる。本稿の圧縮方式であっても圧縮後のサイズは変わらない。
しかし、本論文によれば、2つの点をまとめて圧縮する際のアルゴリズムを工夫することで 点を個別に復元する際の計算量よりも少ない計算量で同じ復元が行えることになる。
なお下記のテーブルの通り、圧縮時の計算量はむしろ2回のinvmod操作が必要なため増えていることに注意せよ。
復元時に必要なべき乗算(exp)の削減が、それを上回る効用をもたらす場合にのみ本論文は意味がある。
この二重点圧縮の特徴
要素Z \in F_qの-6乗を扱う。
これはq \equiv 3 \ (mod\ 4), q \not\equiv 1\ (mod\ 27)のときF_qでの指数化が一回のみでできるということを利用するためである。
古典的な方法であると二回必要。
二重点圧縮
ここで、n \in Z/6は、要素z:= x_1y_1 \in F_qの位置番号である。
条件\phi_k(P_0) = P_1は、同型写像\phiがF_q上に定義されている場合、つまりβ^{-6} \in F_qが成り立つ場合である。
二重点の復元
アルゴリズムを追うと復元時の計算量がナイーブに計算した場合より少ないことが分かる。
圧縮テクニックの拡張
他の楕円曲線の形式であっても有効な場合がある。
E_a : y^2 = x^3 + ax ,j-不変量1728, q \equiv 1\ (mod\ 4)
の場合でも次数4のF_q同型写像がE_a上に存在するため、この圧縮テクニックは使用可能である。
コメント
この論文で話題になっている楕円曲線(E_b: y^2 = x^3 + b)にはビットコインで使われているsecp256k1も当てはまります(b = 7)。
ビットコインの場合楕円曲線上の点の圧縮を行うのは主にアドレス作成時のユーザーであり、検証を行うのは全フルノードクライアントであるため一見この方法が有効そうですが、ユーザーが2つの公開鍵を同時に用意するというシチュエーションが中々無さそうです。
もしもマイナーがブロックを生成するタイミングでトランザクションに含まれる全ての公開鍵をこの方式で圧縮するような仕組みができれば、フルノードの検証速度が向上するメリットはありそうなので、署名検証のバッチ化の一つの案として考えておくのは良さそうだと思いました。
参考
- j-普遍量の定義や具体的な計算方法については https://ja.wikipedia.org/wiki/J-%E4%B8%8D%E5%A4%89%E9%87%8F#%E4%BB%A3%E6%95%B0%E7%9A%84%E5%AE%9A%E7%BE%A9 を参照。secp256k1では0になると分かる。