はじめに
ビットコインを始めとする暗号通貨は、その名前の通り暗号を利用しています。
計算複雑性理論はP, NPといった計算問題の複雑性のクラスを扱う理論ですが、暗号理論はこの計算複雑性理論の中の未解決の問題の上に成り立っています。
計算複雑性理論、暗号理論の核心的な仮定を列挙し、この世界の可能性を分類したものがイムパグリアツォ(Impagliazzo)の5つの可能世界 1と呼ばれています。
ビットコインの最も基礎のレイヤーである署名やハッシュ関数などもこの仮定の影響を受けることになります。
この記事のタイトルに対する回答を結論から言ってしまえば、「超えるべきハードルが多いのであまり解明できていない」というのが答えになってしまいます。しかし、基本的には分かっていないことばかりですが、minicrypt = cryptomaniaをどのように証明するかという問題について、アプローチを探る論文234を紹介します。
わかっていること
- 現在のビットコインが依存している仮定はcryptomania。ECDSAを使っているため。
- 単純な形態の暗号通貨を成立させるために必要な最低限の仮定(署名、PoW)は minicrypt で実現可能。
暗号通貨の安全性に影響しそうな未解決問題(重要だと思う順)
以下、量子計算機は考慮に入れていません。
- この世界がminicrypt(またはcryptomania)かどうか
- もしこの世界がminicrypt(またはcryptomania)だとわかれば、少なくともビットコインの暗号学的構成が暗号理論上は可能になる。ただし、この世界がminicryptであると証明することは、少なくとも P≠NP問題(50年以上未解決の数学上の難問)よりも難しい。すぐに解決しそうな問題ではない。
- この世界がminicrypt(またはcryptomania)だと仮定して、現在使われている具体的なハッシュ・署名アルゴリズムが安全かどうか
- 理論上構成できるかと、実際に使えるものが見つかるかは別の問題になる。SHA256(d)やECDSA, Schnorr署名がそれに当たるかは不明で、現状は安全性の証明もない。すぐに解決しそうな問題ではないし、歴史的にはむしろハッシュ関数はいずれ危殆化するものと考えられる。
- ハッシュ関数から公開鍵暗号を実現する方法 (minicrypt = cryptomania)
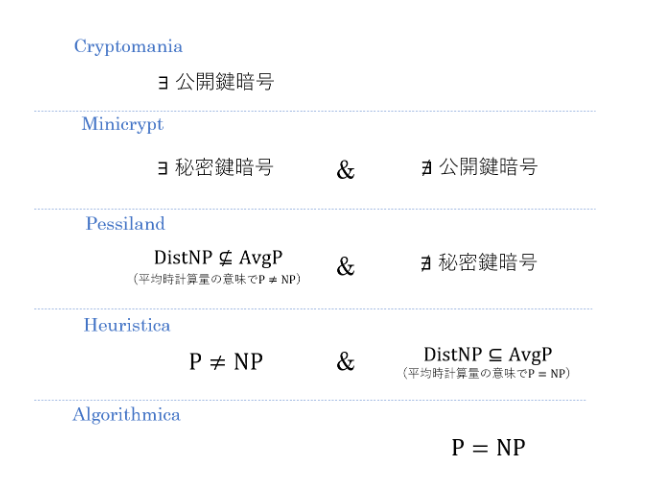
図(5より) : 計算量理論の現在の知識と一貫性のある五つの可能世界。ちょうど一つが我々の真の世界に対応する。予想では、Minicryptの中の道具だけをつかってCryptomaniaを実現できるとされている。
minicrypt = cryptomaniaをどのように証明するか?
ハッシュ関数から鍵交換アルゴリズムなどを構成できることが示せれば、minicrypt = cryptomania が証明できることになる。
ブラックボックス的な手法ではハッシュ関数から鍵交換アルゴリズムが導出できないことが知られている6。ブラックボックス的な手法というのは、ハッシュ関数の内部を観測・操作することができず、入出力だけが観測できる道具としてのみハッシュ関数を扱えるような手法である。
例えば、ランポート署名7は入出力を観測する道具としてのみハッシュ関数を使っているのであり、ハッシュ関数の中身に触れていない。そのため、署名アルゴリズムはブラックボックス的な手法でハッシュ関数から導出できると言える。
以下のいずれのアプローチも、「何らかの存在するかもしれない手法」と ハッシュ関数 から紛失通信(oblivious transfer, OT)を構成することで示そうとしている。OTはcryptomaniaに属することが知られている。
なお、以下では OT, PIR等のアルゴリズムが特に断りなくsemi-honestモデルやhonest-but-curiousモデルで記述されているが、それらは別途悪意のある攻撃者に対応するモデルに変換できることが知られている。
ハミルトン閉路を使ったアプローチ
論文4の「Theorem 7」の解説になる。
秘密分散法と言えば、実用的には「シャミアの秘密分散法」のような、n人のうちt人が揃えば秘密情報の回復が許可されるような秘密分散法を指すことが多い。
しかし、もっと一般的には、n人のプレイヤーを集合と捉えて、その部分集合に対して個別に秘密情報の回復を許可するかどうかを判定するアクセス構造(access structure)であると考えることができる。例えば {A, B, C, D} の4者に対して 集合{A, B, C}, {A, B}, {B, C}, {C, D}, {A}, {D} のみが復号できるといった複雑な条件などが可能である。このような条件のとき、アクセス構造\cal{A}に対して \text{\{A, B, C\}} \in \cal{A}, \text{\{A, B, D\}} \notin \cal{A}のように書く。
秘密分散におけるn人のプレイヤーを完全無向グラフG = (V, E)の辺に割り当てたとき、興味深いアクセス構造を定義できる。完全無向グラフとはノードの集合Vと辺の集合Eからなるグラフで、全てのノードが辺によって結ばれている無向グラフのことであり、ノードの数 |V| = mとすると辺の数n = |E| = \begin{pmatrix} m \\ 2 \end{pmatrix}となる。
グラフの辺の部分集合Tが、グラフGにおいてノードv_1とv_mをつなぐ経路になっている場合(無向到達可能性問題=USTCONと呼ばれる問題であり、これの解があるケース)にのみアクセスを許可し、そうでない場合にはアクセスを許可しないようなアクセス構造 \cal{A}_\text{ustcon}を考えることができる。このようなアクセス構造に対して、効率的に秘密分散を行うためのアルゴリズムが知られている。
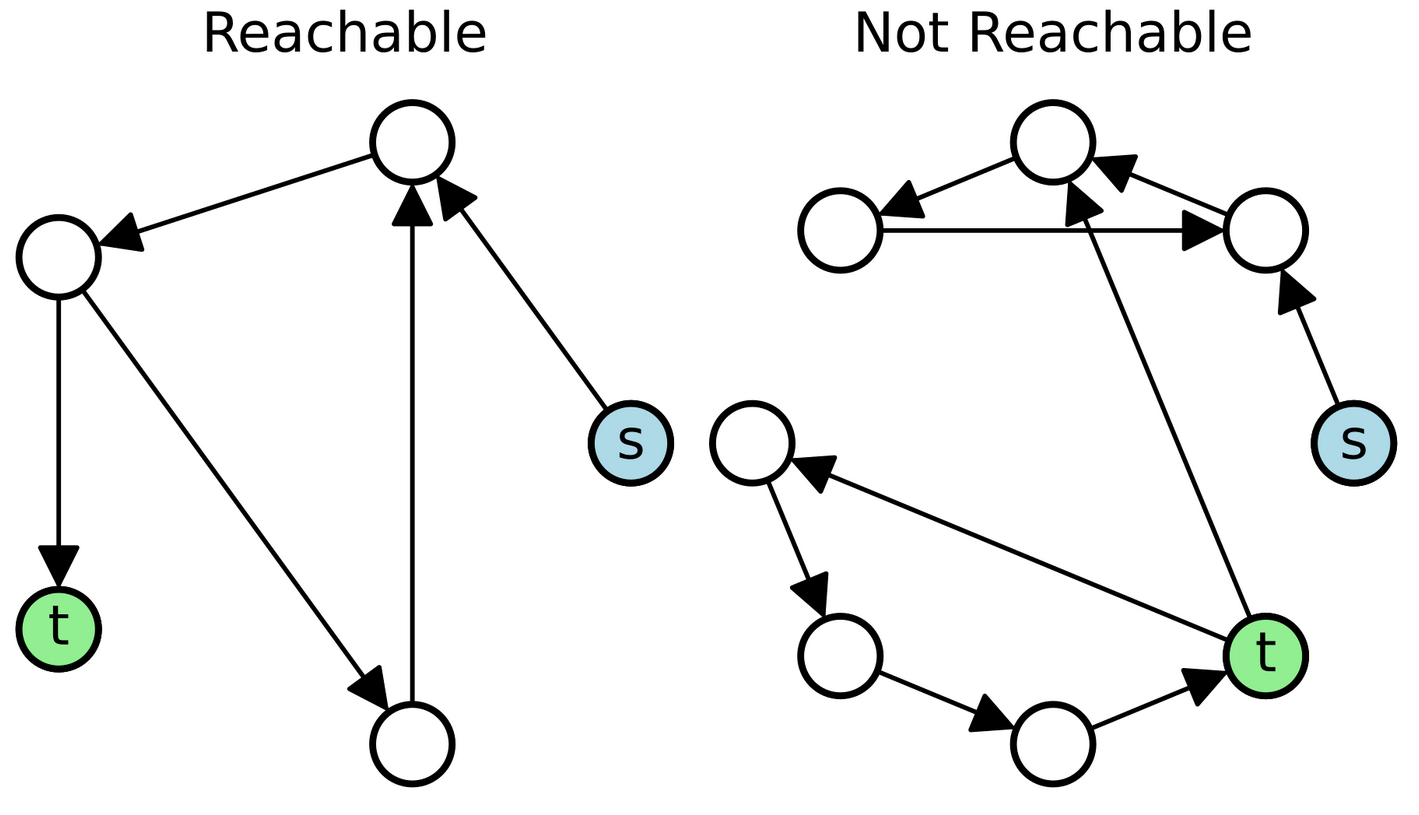
以下は8より、有向到達可能性問題=STCONの図。これを無向にしたものがUSTCON問題。
ustconアルゴリズム
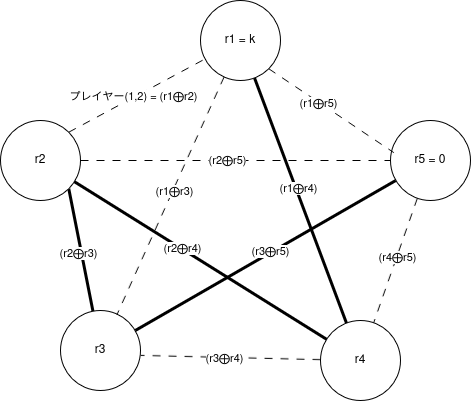
秘密情報(ビット)を k \in \{0,1\}とする。ディーラーはm-2個のランダムなビットr_2, .., r_{m-1}を生成する。また、r_1 = k, r_m = 0とする。
これらの値を使って、辺(v_i, v_j)に対応したプレイヤーの持つ値を r_i \oplus r_jとすることで、秘密分散とする。
以下の図はustconアルゴリズムでv1からv5まで到達可能であり、\cal{A}_\text{ustcon} に受理されるようなグループの例。ここでいうプレイヤーは (v1, v2), ..., (v4, v5)の10人であり、以下の図ではプレイヤー10人のうち(v1,v4), (v2, v4), (v2, v3), (v3, v5)の4人が所属している集合によって、秘密回復ができることになる。
問題は、このような単純な方法が本当に秘密分散になっているかどうかである。
詳細は論文4の 3.2 Undirected s-t-Connectivity を参照してほしいが、秘密分散になっているかの判定方法として、以下のような手段があることに注目する。
\cal{A}_\text{ustcon}に含まれる集合TについてはT内の各プレイヤーに割り当てられるシェアを使うことで確実に秘密kが回復できる。\cal{A}_\text{ustcon}に含まれない集合Tについて、ディーラーが生成する乱数を固定しておく。k=0の場合とk=1の両方において、T内の各プレイヤーに割り当てられるシェアの値が一致しているならば、T内の各プレイヤーはkに関する情報を全く得られていないことになるため、秘密kは回復できない。
この手法を使って、より重要な問題を扱うことになる。
効率的シェア分配の困難性
上記同様にグラフの辺の部分集合Tが、グラフGのハミルトン閉路9になっている場合に アクセスを許可し、そうでない場合にはアクセスを許可しないようなアクセス構造 \cal{A}_\text{ham}を考えることができる。
\cal{A}_\text{ustcon} ではディーラーが効率的に(多項式時間で)秘密分散を行い、プレイヤーが効率的に秘密情報を回復することができたが、\cal{A}_\text{ham}においてはそのような効率的な操作が行えるだろうか?この問題は解決されていないが、以下の定理6によりそのような効率的な秘密分散は行えないだろうと予想されている。
定理6: ハミルトン閉路アクセス構造に対する(情報理論的に)効率的な秘密分散スキームとNP, co-NPの関係
もしも NP ≠ co-NP であるならば、
\cal{A}_\text{ham}に対する効率的な秘密情報の回復アルゴリズムは存在しない。
NP = co-NP は P = NPとは別の問題であるが、 NP = co-NP が成り立つと(一般に崩壊しないと信じられている)多項式階層10が崩壊してしまうため、 NP ≠ co-NP は一般に正しいと考えられている。
定理6の証明
\overline{\text{HAM}}を\{G: G\text{はハミルトン閉路を含まない}\}のような集合として定義する。 「\cal{A}_\text{ham}に対する効率的な秘密情報の回復アルゴリズムが存在する」と仮定すると、NP = co-NP が成立してしまうことを示す。
ハミルトン閉路問題の補問題、すなわち「与えられたグラフにハミルトン閉路が存在しないこと」を判定する問題は、co-NP完全に属することが知られている。この問題が、さらにNP問題であることを示せば NP = co-NP が成立する。NP問題の定義とは、証拠wが与えられたときに多項式時間で正しさを検証できるような問題であり、 \cal{A}_\text{ham}に対する効率的な秘密情報の回復アルゴリズムが存在すると、ハミルトン閉路問題の補問題に対してそのような証拠wを作成できてしまうことを示す。
(完全グラフとは限らない)グラフ G = (V, E)がハミルトン閉路を含まないとすると、Eに対して E \notin \cal{A}_\text{ham}になる。これはすなわち、Vを頂点とする完全グラフを使った秘密分散スキームにおいて、Eに相当するプレイヤーの集合が秘密情報を回復できないということを意味する。
さらにこのとき、「\cal{A}_\text{ham}に対する効率的な秘密情報の回復アルゴリズムが存在する」という仮定から、Eに相当するプレイヤーの集合に対して k = 0 のケースと k = 1 のケースにおいて、乱数を固定した場合には同じ値が回復されるようなアルゴリズムAが存在することになる。
アルゴリズムAを使ってk = 0 のケースで回復された値を r_0とし、k = 1のケースで回復された値を r_1とする。ここで、グラフGが与えられたときに、G \in \overline{\text{HAM}} であることを検証するための証拠wを、r_0, r_1とすれば、「ハミルトン閉路問題の補問題」の証拠w(E \notin \cal{A}_\text{ham}ならばr_0 = r_1となる )が作成できたことになるため、「ハミルトン閉路問題の補問題」はNPに属することになる。
注意: アルゴリズムAは、Eが与えられたときにハミルトン閉路問題の補問題を効率的に解くためのアルゴリズムではない。答えが与えられた時の検証のためのアルゴリズムとしてアルゴリズムAを使っている。検証者は問題のグラフG = (V, E)に加え、各プレイヤーに相当する辺に割り当てられた固定された乱数、r_0, r_1、アルゴリズムAを与えられればその答えを検証できる。
ハミルトン閉路アクセス構造に対する(計算量的に)効率的な秘密分散スキーム
上で説明した通り、無条件に(情報理論的に)効率的な、ハミルトン閉路アクセス構造に対する秘密情報の回復アルゴリズムを探すのは難しいということが分かっている。
しかし、この条件を緩和して、「計算量的に」効率的なハミルトン閉路アクセス構造を定義すると一方向性関数(OWF)から紛失通信(OT)が導けることが分かっている。
ハミルトン閉路アクセス構造に対する「計算量的に」効率的な秘密分散スキームは以下の性質を持つ。
- アクセス構造に対して、秘密分散アルゴリズムと、回復アルゴリズムが「秘密文字列の長さ」「プレイヤー数」について多項式時間で実行できる
- 攻撃者は、多項式時間チューリングマシンであり、アクセス構造によって許可されていない集合に含まれるプレイヤーをコントロールすることができる。この攻撃者は、秘密情報Aを分散させて作ったシェアと、別の秘密情報Bを分散させて作ったシェアを見分けることができない
- (要するに、秘密情報に関する情報を得ることができない)
ここで、\cal{A}_\text{ham}に対する効率的な秘密情報の回復アルゴリズムAとして以下のような、条件の緩いものを考えてみる。
グラフの辺集合Eに対応するプレイヤーは、辺集合Eを使ってハミルトン閉路を構成する方法を与えられたならば、アルゴリズムAを使って秘密情報を効率的に回復できる。
このような秘密情報回復アルゴリズムAは未だに存在が立証されていないが、プレイヤーはハミルトン閉路を構成するための答えを予め与えられているのだから、アルゴリズムAを構成することは不可能ではなさそうに思える。
このようなアルゴリズムAが存在すると仮定した上で 1-of-2 OT を構成することができるというのが、次の定理7の主張である。
定理7: ハミルトン閉路アクセス構造に対する秘密分散スキームを使った minicrypt = cryptomania の導出
\cal{A}_\text{ham}に対する効率的な秘密分散スキームと、一方向性関数を使って 1-of-2 OT を構成することができる.
OTは cryptomaniaに属するため、ハッシュ関数のみからcryptomaniaのプリミティブが作成できたことになり、minicrypt = cryptomaniaが成立する。
定理7の証明
\text{Gen}をlビットの入力を2lビットに拡張するような疑似乱数生成器とする。一方向性関数が存在すれば、そのような疑似乱数生成器は構成可能である。
言語 L_{\text{Gen}} = \{ y: \exists x\ \text{Gen}(x) = y \}を考える。L_{\text{Gen}}は証拠x = wを使って検証できるから、NPに属する。fをL_{\text{Gen}}からハミルトン閉路問題に多項式時間帰着させる変換関数とする。
すなわち以下の2つを満たす。
- fは多項式時間で計算できる。
- ハミルトン閉路を含むグラフ全体の集合を
\text{Hamiltonian}として、y \in L_{\text{Gen}}はG = f(y) \in \text{Hamiltonian}と同値である。
このような関数fはさらに、以下の性質も持つ。 - yに対する証拠xはfを使って
G = f(y)に対する証拠に効率的に変換できる。すなわち、 以下を与えられたときにGにおけるハミルトン閉路を多項式時間で探し出すことができる。y \in L_{\text{Gen}}- その証拠となるx(つまりそれは y = Gen(x)となるときである)
G = f(y)
以下のプロトコルが 1-of-2 OTのプロトコルである。
- 受信者の入力:
i \in \{ 0, 1\}とセキュリティパラメータ1^l - 送信者の入力:
b_0, b_1とセキュリティパラメータ1^l - 受信者の行動1
- 乱数
x_1 \in \{0,1\}^lを選択し、y_1 = \text{Gen}(x_1)を計算する - 乱数
y_0 \in \{0,1\}^{2l}を選択する \sigma \in \{0,1\}に対してG_{\sigma} = f(y_{\sigma})を計算- i=0ならば
(G_1, G_0)を送信者に送信する。i = 1ならば(G_0, G_1)を送信者に送信する。
- 乱数
- 送信者の行動1
H_0 = (V_0, E_0), H_1 = (V_1, E_1)を受信者から送信されたグラフとする。j \in \{0,1\}に対してビットb_jをアクセス構造\cal{A}_\text{ham}に対する秘密分散スキームを用いてV_jをノードとする完全グラフの辺に対応するように分割する。さらに、完全グラフの辺の部分集合であるE_jに対応するプレイヤーに割り当てられた秘密分散シェアの集合S_jを受信者に渡す。
- 受信者の行動2
x_1, y_1を使ってG_1 = H_iにおけるハミルトン閉路を計算する。さらにこの閉路の秘密分散シェアの集合S_iを使って、ビットb_iを回復する。送信者から送られたビットはb_iとなる。
送信者の持つビット b_{\overline{i}}については、「受信者も答えを知らないハッシュ関数の入力」に対応しており、受信者は対応する秘密分散シェアを与えられてもハミルトン閉路を計算することが出来ないので、ビットの回復もできない。
NPインスタンスの圧縮を使ったアプローチ
詳細は論文11を参照。
NP完全問題の中には、問題の入力サイズを圧縮できるものがあることが知られている。
代表的なものは頂点被覆問題12である。頂点被覆問題は入力であるグラフ(V, E)に加えてパラメータkを取るが、問題のサイズをO(k^2)に変換できることが知られている13。もしkがグラフ(V, E)のサイズ(ノード数、辺数)と比べて小さければ、問題のサイズを圧縮できることになる。
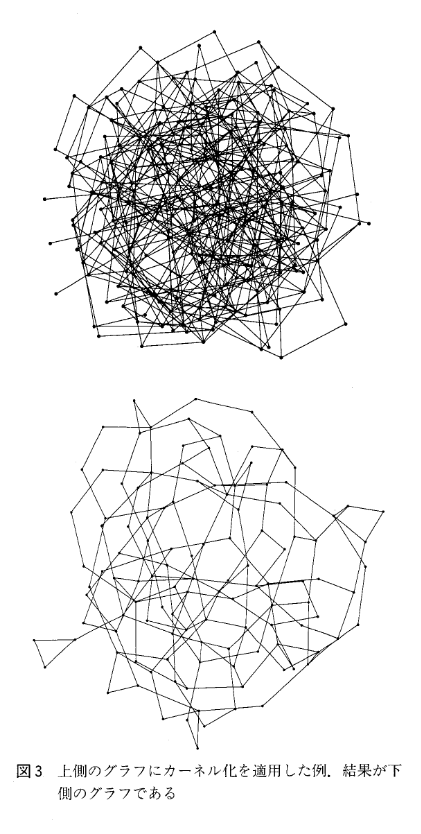
以下の図は頂点被覆問題のサイズを圧縮する「カーネル化」と呼ばれる手法により、グラフサイズの圧縮を可視化したもの(13より)。
頂点被覆問題はNP完全問題であることが知られている。さらに、他の「最小フィルイン問題」「疑似乱数生成器を使った問題」も同様にNPに属する問題であり、同様にサイズを圧縮するアルゴリズムが知られている。
よって、原理的にはSATなど他のNP完全問題も多項式時間で頂点被覆問題に還元できるので、このような圧縮が適用できそうに思えるが、単純に還元 -> 圧縮を適用するだけでは問題サイズの圧縮にはならない。
論文11では、W還元(W-Reduction)という問題の還元手法が存在すると仮定して、もしその還元手法が存在したならば、新しい問題クラスを定義することができ、さらに還元前の問題が圧縮可能ならば、還元後の問題も圧縮可能になると説明している。(具体的にW還元を構成しているわけではない)
証拠(witness)の保存性
NP問題の検証に使うことができる証拠wを考える。もとの問題を圧縮することができたとする。圧縮した後の問題を検証するための証拠をw'とする。wの知識を持つ検証者が、w'を使って圧縮後の問題を検証することができるとき、このような圧縮を「証拠保存可能圧縮 (witness retrievable compression)」と呼ぶことにする。
(現在は判明していないが)SATを証拠保存可能圧縮する手法が存在したとする。この圧縮手法と、一方向性関数(OWF)を使うと、PIR(private information retrieval; 秘密情報取得)が構成できる (以下11の定理3.1)。PIRはOT(oblivious transfer; 紛失通信)に、OTは鍵交換アルゴリズムに変換することができ、ここから minicrypt (OWF) = cryptomania であるといえることになる。
定理3.1の方法ではハッシュ関数(OWF)を具体的な回路として書き直し、それをNP問題とみなしてSATで表現するところから始める。したがって、この方法はブラックボックスではないことになる。
定理 3.1. SATの証拠保存可能圧縮を利用したOWFによるPIR実現
SATに対して、証拠保存可能圧縮が存在するとき、OWFからPIRを実現することができる。
定理3.1.の証明
アリス(PIR送信者)とボブ(PIR受信者)を考える。ボブはm個のレコードを持つデータベースDのPIRにおいてi番目のビットを取得したいとする。ボブの選択したインデクスi \in [m]をビット分解した表現を i_1, i_2, ..., i_lとする。i番目のデータベースの要素をD[i]とする。
アリスは入力としてDを持ち、ボブは入力としてiを持つ。
非自明なPIRを実現するためには、アリスはボブに対して長さm未満のデータしか渡さないにも関わらず、ボブがD[i]を取得できなければならない。
- ボブは乱数
r_Bを生成し、インデクスiのコミットメントを作成する。アリスはコミットメント\sigma = \text{Commit}(i, r_B)を受け取る。 - アリスはSATインスタンスΦを作成する。ΦのCNFは以下の通り。
- 入力
\sigmaを固定したコミットメント検証アルゴリズムを\text{Verify}_\sigmaとする。\text{Verify}_\sigmaは入力としてx, rを受取り、コミットメント\sigmaと一致したら1となる。 \text{Verify}_\sigmaをCNFに変換したものを\Phi_{\sigma}とする。このCNFの入力はxのビットx_1, x_2, ..., x_lと入力乱数rのビットである。それぞれ、ボブは既に手元で生成しているものであり、アリスは知らないがx = i, r = r_Bであるj \in [m]に対して、C_jを以下のように定義する。- もし D[j] = 0 ならば:
C_j = ({x_1}^{\overline{j_1}} \lor {x_2}^{\overline{j_2}} \lor ... \lor {x_l}^{\overline{j_l}} )(ここで、x^0 = \overline{x}, x^1 = xとする) - もし D[j] = 1 ならば:
C_j = 1
- もし D[j] = 0 ならば:
\Phi = \Phi_{\sigma} \land (\bigwedge_{j \in [m]} C_j )
- 入力
- アリスは
\Phiを圧縮して\Psiとし、ボブに\Psiを送る。 - ボブは
\text{Verify}_\sigmaの 証拠を知っているので、\Phi_{\sigma}の証拠wも計算できる。ボブは\Psiを検証し、\Psiにwを適用した値を導出する。検証に成功したならば D[i]の値は1であり、検証に失敗した場合D[i]の値は0になる。
注意: これは OT ではなく PIRなので、ボブは厳密には\Psiを解読することでその他のデータベース内の要素に関する情報を得られる可能性がある。しかし圧縮後の問題\Psiのサイズn に対してデータベースサイズmを十分に大きく取れば、非自明なPIRを構成することが出来ていると言える。
PIRとして、プロトコルに従うことでボブは確実にD[i]を入手できる。また、ボブがアリスに送信する情報はコミットメントだけであるため、アリスはボブの情報を何も知ることはできない。したがって、OWFからPIRを実現することができている。
おまけ
- pessilandでは機械学習が効率的に行える14(直感的には 一方向性関数がない = 学習を妨害するような問題が存在しない)
- この世界がcryptomaniaだった場合は役に立つが、minicryptだった場合は役に立たないようなものは数多く存在する(例: 公開鍵暗号)。一方で、cryptomaniaでは役に立たないが、minicryptにおいてのみ役に立つ結果が得られるケースもある15。(例: 直列に繋いだ非適応的一方向性関数の適応的安全性は、minicryptにおいてのみ得られる。簡単に言うと、minicryptの世界では「弱い」ハッシュ関数を2回連続で適用したものを「強い」ハッシュ関数として利用することができるが、cryptomaniaの世界ではこれが成り立たない)
- 万が一、大方の予想に反してこの世界がminicryptではない(つまりalgorithmica, heuristica, pessilandのいずれかである)ということが証明されてしまったとしても、現実的にハッシュ関数を破る構成ができないような証明であったならば、現在稼働している暗号通貨に対する影響は大きくない可能性もある。単に予想が解決されれば安全/危険が決まるという訳ではなく、以下のような複雑な状況にもなりうる。
- 安全な暗号通貨を構成する方法は存在しないことが証明される(つまりalgorithmica, heuristica, pessilandのいずれかである)が、実用上既存のECDSA/SHA256を破る方法を見つけることもできない。
- 安全な暗号通貨を構成できることが証明される(つまりminicrypt, cryptomaniaのいずれかである)が、同時に実用的なECDSA/SHA256などのアルゴリズムには全て脆弱性が見つかり、さらに実用的な代用も見つからない。
参考文献
-
あなたの身の回りの暗号は大丈夫?計算量理論と暗号の世界 https://www.nii.ac.jp/event/upload/nii_shimin_hirahara_20210225.pdf ↩
-
Secret-Sharing for NP https://www.wisdom.weizmann.ac.il/~naor/PAPERS/secret_sharing.pdf ↩ ↩
-
How to Prove that Minicrypt=Cryptomania (in the future) or Secret Sharing for Access Structures beyond P https://www.wisdom.weizmann.ac.il/~naor/PAPERS/minicrypt.html ↩ ↩
-
Secret-Sharing Schemes: A Survey https://www.researchgate.net/publication/220776045_Secret-Sharing_Schemes_A_Survey ↩ ↩ ↩
-
「メタ計算量理論」について https://researchmap.jp/shuichi.hirahara/misc/31537816/attachment_file.pdf ↩
-
ブラックボックス構成とその限界 https://tcc.c.titech.ac.jp/yasunaga/talks/crypto_school_BB201309.pdf ↩
-
ランポート署名 https://ja.wikipedia.org/wiki/%E3%83%A9%E3%83%B3%E3%83%9D%E3%83%BC%E3%83%88%E7%BD%B2%E5%90%8D ↩
-
st-connectivity https://en.wikipedia.org/wiki/St-connectivity ↩
-
ハミルトン閉路問題 https://ja.wikipedia.org/wiki/%E3%83%8F%E3%83%9F%E3%83%AB%E3%83%88%E3%83%B3%E9%96%89%E8%B7%AF%E5%95%8F%E9%A1%8C ↩
-
多項式階層 https://ja.wikipedia.org/wiki/%E5%A4%9A%E9%A0%85%E5%BC%8F%E9%9A%8E%E5%B1%A4 ↩
-
On the Compressibility of NP Instances and Cryptographic
Applications https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=841339ae898a50eb7caf731e413826a82a38da0c ↩ ↩ ↩ -
頂点被覆 https://ja.wikipedia.org/wiki/%E9%A0%82%E7%82%B9%E8%A2%AB%E8%A6%86 ↩
-
固定パラメータ容易性: https://orsj.org/wp-content/corsj/or52-9/or52_9_535.pdf ↩ ↩
-
Learning in Pessiland via Inductive Inference https://eccc.weizmann.ac.il/report/2023/100/ ↩
-
Composition Implies Adaptive Security in Minicrypt https://iacr.org/archive/eurocrypt2006/40040330/40040330.pdf ↩