Bech32 のチェックサム

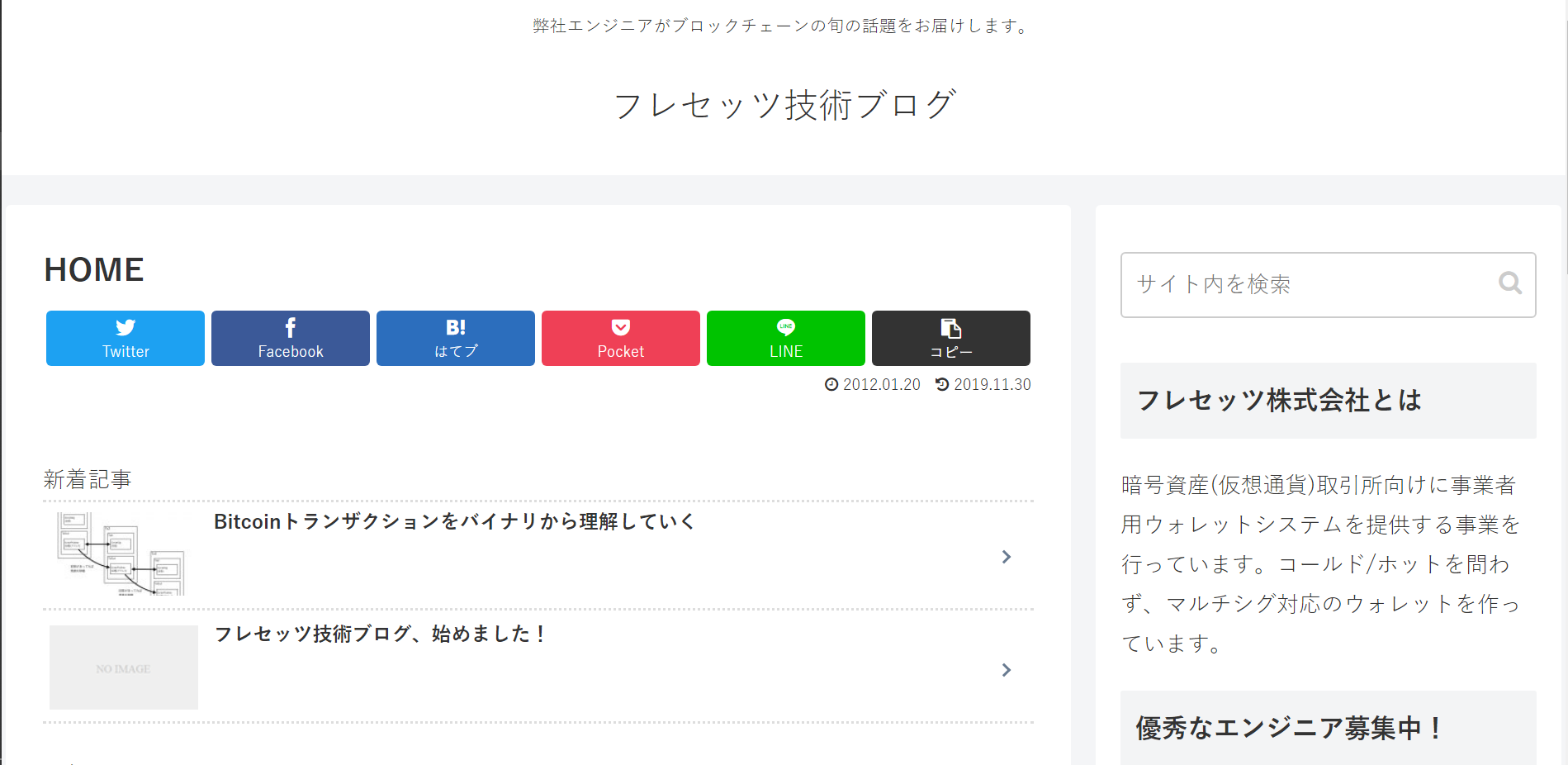
Bech32 のチェックサム

segwit アドレスなどに使われる Bech32 エンコードは BIP-173 に記述されています。
この記事では、チェックサム部分のアルゴリズムを解いていきます。

BIP ではまず python のソースコードで示されています。
加えて、これは BCH符号であり、各種パラメータを決めた理由も色々挙げられています。

1 def bech32_polymod(values):
2   GEN = [0x3b6a57b2, 0x26508e6d, 0x1ea119fa, 0x3d4233dd, 0x2a1462b3]
3   chk = 1
4   for v in values:
5    b = (chk >> 25)
6    chk = (chk & 0x1ffffff) << 5 ^ v
7    for i in range(5):
8      chk ^= GEN[i] if ((b >> i) & 1) else 0
9  return chk

bitcoin-core のソースコード にはもうちょっと詳しくコメントが書かれています。
これを手掛かりにもう少し深く理解したいと思います。

有限体 GF(2), GF(32)

BCH 符号は有限体の剰余になります。有限体 GF(q) は、要素数が q で要素間の四則演算の結果もまたその集合の要素になるような集合です。
Bech32 では、GF(32) と GF(2) が使われているので、これらの性質をさらっておきます。

GF(2)

まず GF(2) は 2の剰余体で表されます。整数を 2 で割った余りに丸めたものです。
たとえば整数の範囲ですと 1+1=2 ですから、結果の 2 を 2 で割った余りの が GF(2) での結果となります。
2の剰余ですよという意味で、\pmod2 を追記して、1+1=0 \pmod2 と書きます。
差は和の逆演算です。2 の剰余体の場合は和と同じになります。
さらに 0,1 をビットとみなすと、和や差は xor と同じ演算になります。

GF(32)

続いて GF(32) ですが、これは係数が GF(2) の要素からなる多項式の集合を、5次の素な多項式で割った余りで表せます。
Bech32 では a^5 + a^3 + 1 を用いているようです。
5次式で割った余りなので、結果は 4次になり、係数は(ゼロ次の項を含めて) 5つあります。
この係数を並べて書くと、例えば a^4 + a^3 + a は 11001 と表記することができます。
bitcoin-core のコメントではこれを二進数とみなして簡易的に十進数で表記しています。整数と区別するため \{\} でくくり、\{25\} と書きます。

GF(32) の和

GF(32) の要素の和を考えましょう。
多項式ですから、和は同じ次数の係数同士で和をとればよいです。
たとえば (a^4+a^3+a+1) + (a^3+a^2+1) は、1+1=0 \pmod2 なことに注意して、

   (a^4 + a^3 + a + 1) + (a^3 + a^2 + 1) \\
\begin{aligned}
 =\quad& a^4 &+&(1+1)a^3 &+& a^2 &+& a &+& (1+1) \\
 =\quad& a^4 & &         &+& a^2 &+& a & & \\
\end{aligned}

係数のビットベクトル表記なら、各桁独立に xor すればよいので、普通の二進数の xor と同じです:

\begin{aligned}
a^4 + & a^3   &     &+ a &+ 1&\quad\rightarrow 11011 \\
      & a^3 + & a^2 &    &+ 1&\quad\rightarrow 01101 \\
\end{aligned} \\
  11011 \ xor \ 01101 = 10110 \quad\rightarrow a^4+a^2+a

これを十進数で書けば、bitcoin-core のコメントにあるように、

\{27\} + \{13\} = \{27 \ xor\ 13\} = \{22\}

が得られます。

GF(32) の積

次に積ですが、これは素直に多項式の積を計算して a^5 + a^3 + 1 で割った余りを取ります。

\begin{aligned}
\{5\} * \{26\}=\ & (a^2 + 1) * (a^4 + a^3 + a) \\
              =\ & (a^4 + a^3 + a) * a^2 + (a^4 + a^3 + a) \\
              =\ & a^6 + a^5 + a^4 + a \\
              =\ & a^3 + 1 \pmod {a^5+a^3+1} \\
              =\ & \{9\} \\
\end{aligned}

BCH符号計算のアルゴリズム

Bech32 の BCH符号パラメータ

BCH符号は、有限体の剰余でした。
有限体の大きさや、剰余に使う多項式(=生成多項式)は、エラーの発見能力で制限されます。

BIP-173 にあるように、Bech32 では 1023文字中の 3つのエラーを発見する能力を選びました。
このことから、用いる有限体は GF(1024) = GF(32^2) に決まります。

生成多項式は GF(32) を係数とする 2次の多項式 3つの積になります(正しくは、連続する原始多項式3つの最小公倍数)。
これは g(x) = x^6 + {29}x^5 + {22}x^4 + {20}x^3 + {21}x^2 + {29}x + {18} になるようです。

BCH 符号計算のアルゴリズム

入力データを GF(32) を係数とする多項式とみなし、それを g(x) で割った余りを計算します。
5bit を GF(32) の要素とみなして扱います。

多項式の除算ですが、これは筆算を想像してください。
例として、整数係数の多項式の除算、(12x^3 + 11x^2+7x+5) / (3x+2) を考えましょう

\begin{aligned}
            &       &   4x^2  &+&  1x &\\
  3x+2 \ /\ & 12x^3 &+ 11x^2  &+& 7x  &+ 5 \\
            & 12x^3 &+  8x^2  & &     & \\
            &       &  3x^2   &+& 7x  & \\
            &       &  3x^2   &+& 2x  &\\
            &       &         & & 5x  &+ 5 \\
\end{aligned}

(12x^3 + 11x^2 + 7x + 5) / (3x + 2) = 4x^2 + 1x \ ,,,\ 5x+5 と計算できました。

この筆算のアルゴリズムを解析すると、被除数の上から 2項を取り出して除算し、出た余りに次の桁を追加して除算し…と繰り返す形になっています。
GF(32) 係数多項式の余りも同様に計算できます(途中で出てくる掛け算と引き算は GF(32) で行います)

これをソースコードへ書き下すと、一桁ずつ取り出して中間結果に追記するループで書くことができます。
追記は桁をずらしてからの加算なので、シフトして xor でいけます。

3 chk = 1
4  for v in values:
5    b = (chk >> 25)
6    chk = (chk & 0x1ffffff) << 5 ^ v

3行目の初期値の 1 は、入力多項式の最大項の係数を 1 にするためのトリックです。
これが無いと、例えば 101... と 0101... の区別がつかなくなります。

6行目は chk の下 25 ビットを取り出して 5bit シフトし、次の桁の値である v を加えています。
25bit は GF(32) 数を 5つで、それを 5bit つまり GF(32) 一つ分ズラし、下一桁に v を入れているので、つまり chk は GF(32) 数を6つ、5次多項式の係数リストです。
6次の係数は 5行目で b に保持されています。

l(x) を 5次多項式として被除数 c(x) を b*x^6 + l(x) と置き、6次多項式 g(x) での余りを計算すると、

\begin{aligned}
  c(x) \pmod{g(x)} &=& (b*x^6 + l(x)) \pmod{g(x)} & \\
                   &=& (b*x^6 \pmod{g(x)}) & \ +\ (l(x) \pmod{g(x)}) \\
\end{aligned}

l(x) は 5次なので、6次式で割った余りは自分自身だから、

\begin{aligned}
  c(x) \pmod{g(x)} &=& (b*x^6 \pmod{g(x)}) & \ +\ l(x) \\
\end{aligned}

つまり、6次の項を g(x) で割った余りに、5次以下の項を加えたものになります。
ソースコードで言えば、6 行目の chk は l(x) に相当します。これに 5行目の b は式中の b に相当します。
つまり chk に b*x^6 \pmod{g(x)} を加えればよいわけです。

次の問題は、b * x^6 \pmod{g(x)}です。
b は GF(32) の要素なので 5bit のベクトルで表すことができます。
これを b = (b4, b3, b2, b1, b0) とすると、

\begin{aligned}
 b * x^6 \pmod{g(x)} &\ =\ & (b4, b3, b2, b1, b0) * x^6 \pmod{g(x)} \\
                     &\ =\ & (b4, 0, 0, 0, 0) * x^6 \pmod{g(x)} \\
                     & & +\ (0, b3, 0, 0, 0) * x^6 \pmod{g(x)} \\
                     & & +\ (0, 0, b2, 0, 0) * x^6 \pmod{g(x)} \\
                     & & +\ (0, 0, 0, b1, 0) * x^6 \pmod{g(x)} \\
                     & & +\ (0, 0, 0, 0, b0) * x^6 \pmod{g(x)} \\
\end{aligned}

ここで b ベクトルの要素は GF(2) の元なので 0 か 1 です。

0 の場合はベクトル全体がゼロ、つまり GF(32) の零元ですから、

\begin{aligned}
  & (0,0,0,0,0) * x^6 \pmod{g(x)} \\
 =& (0,0,0,0,0) \\
 =& \{0\}
\end{aligned}

です。

1 の場合は、

\begin{aligned}
(1,0,0,0,0) * x^6 \pmod{g(x)} &= \{16\}x^6 \pmod{g(x)} \\
                              &= \{16\} * (x^6 \pmod{g(x)}) \\
\\
{\rm 同様に、} \\
(0,1,0,0,0) * x^6 \pmod{g(x)} &= \{8\} * (x^6 \pmod{g(x)}) \\
(0,0,1,0,0) * x^6 \pmod{g(x)} &= \{4\} * (x^6 \pmod{g(x)}) \\
(0,0,0,1,0) * x^6 \pmod{g(x)} &= \{2\} * (x^6 \pmod{g(x)}) \\
(0,0,0,0,1) * x^6 \pmod{g(x)} &= \{1\} * (x^6 \pmod{g(x)}) \\
\end{aligned}

となります。後はこれらを chk に加えればよいわけです。
見やすくするために k(x) = x^6 \pmod{g(x)} と置き、プログラム的に三項演算子を使って書けば、

\begin{aligned}
  b * k(x) &=& ( (b0==0) &?0: ({1} * k(x)) \\
           &+& ( (b1==0) &?0 : ({2} * k(x)) \\
           &+& ( (b2==0) &?0 : ({4} * k(x)) \\
           &+& ( (b3==0) &?0 : ({8} * k(x)) \\
           &+& ( (b4==0) &?0 : ({16} * k(x)) \\
\end{aligned}

これがソースコードの

7    for i in range(5):
8      chk ^= GEN[i] if ((b >> i) & 1) else 0

に相当しているわけです。

GEN の算出

GEN はこう与えられていました。

2   GEN = [0x3b6a57b2, 0x26508e6d, 0x1ea119fa, 0x3d4233dd, 0x2a1462b3]

今までの結果を用いて、GEN を自分で算出することができます。

まず k(x) を計算しておきましょう。

\begin{aligned}
k(x) &=& x^6 \pmod{g(x)} \hspace{230pt}\\
     &=& x^6 \pmod{x^6 + \{29\}x^5 + \{22\}x^4 + \{20\}x^3 + \{21\}x^2 + \{29\}x + \{18\}} \\
     &=& \{29\}x^5 + \{22\}x^4 + \{20\}x^3 + \{21\}x^2 + \{29\}x + \{18\} \hspace{70pt} \\
\end{aligned}

です。

GEN[0]

次に GEN[0] です。これは \{1\} * k(x) なので、k(x) と同じです。
上で求めた k(x) の各係数を 5bit に書き下して連結し、それを二進数値とみなして十六進表記すると、

     {29}  {22}  {20}  {21}  {29}  {18}
->  11101 10110 10100 10101 11101 10010
->  11 1011 0110 1010 0101 0111 1011 0010
->   3    b    6    a    5    7    b    2

2   GEN = [0x3b6a57b2, 0x26508e6d, 0x1ea119fa, 0x3d4233dd, 0x2a1462b3]

GEN[0] に一致しました。

GEN[1]

GEN[0] と同様に、

\begin{aligned}
   GEN[1] &=& \{2\}*k(x) \hspace{330pt} \\
          &=& \{2\} * (\{29\}x^5 + \{22\}x^4 + \{20\}x^3 + \{21\}x^2 + \{29\}x + \{18\}) \hspace{114pt} \\
          &=& \{2\}*\{29\} x^5 + \{2\}*\{22\} x^4 + \{2\}*\{20\} x^3 + \{2\}*\{21\} x^2 + \{2\}*\{29\} x + \{2\}*\{18\} \\
\end{aligned}

GF(32) の積は最初の方で見たように、多項式の積を a^5 + a^3 + 1 で割った余りです。
\{2\} は多項式で表すと一次の項があるだけの x ですから、掛ける多項式を1次上げただけ、ビット表現だと左シフトだけなることに注意して、

\begin{aligned}
  \{2\}*\{29\} &= {00010}*{11101} = 111010 (mod 101001) = 10011 \\
  \{2\}*\{22\} &= 101100 (mod 101001) = 00101 \\
  \{2\}*\{20\} &= 101000 (mod 101001) = 00001 \\
  \{2\}*\{21\} &= 101010 (mod 101001) = 00011 \\
  \{2\}*\{29\} &= 10011 \\
  \{2\}*\{18\} &= 100100 (mod 101001) = 01101 \\
\end{aligned}

並べて十六進表記すると、

   10 0110 0101 0000 1000 1110 0110 1101
    2    6    5    0    8    e    6    d

2   GEN = [0x3b6a57b2, 0x26508e6d, 0x1ea119fa, 0x3d4233dd, 0x2a1462b3]

GEN[1] に一致しました。

あとの GEN も同様に計算できます。