はじめに
この記事ではTaprootの安全性の証明を述べます。 まず、Taprootの歴史、記号の定義、アルゴリズムを述べます。
次に、安全性の証明におけるTaprootのアルゴリズムを定義し、定理を述べ最後にその証明を行います。
Taprootの歴史
Bitcoinのアウトプットに設定されるScriptのサイズを小さくし(効率化)、
不使用のScriptを公開しないよう(プライバシー)提案されたのがTaprootである。
2018年1月に、Bitcoin Core開発者かつBlockstream社の元CTOであるGregory Maxwellにより、Taprootは提案された。
https://lists.linuxfoundation.org/pipermail/bitcoin-dev/2018-January/015614.html
次に2018年4月に、今回扱うAndrew Poelstraによる安全性の証明が公開された。
https://github.com/apoelstra/taproot/blob/master/main.pdf
記号の定義
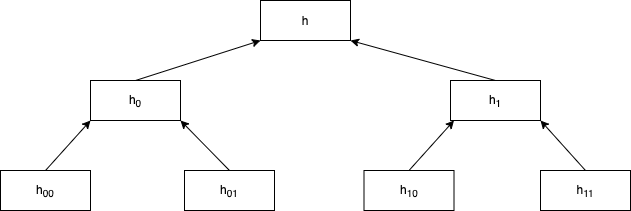
以上のようなマークルツリーを考えるときに、
h=Hash(h_0\|h_1)\\h_0=Hash(h_00\|h_01)\\h_1=Hash(h_10\|h_11)
と表す。
セキュリティパラメータを\lambdaとして
離散対数をオーダーp(\lambda)で解くことができるアルゴリズムが確率neg(\lambda)を除いて存在しない巡回群\mathscr{G}=\langle G \rangleと
アウトプットの長さがq(\lambda)のランダムオラクルとしてモデリングされた2つのハッシュ関数H^{pk},H^mを定義する。
離散対数の定義は以下。
b をGの生成元とすれば、\forall g \in G はk \in \mathbb{N} , g=b^kと表せる。
またgを表現する2つの整数k_1,k_2はnを法として合同だから、
\\log_b:G\rightarrow \mathbb{N}/n\mathbb{N} なる関数を定義でき、bを底とする離散対数と定義する。
また、\beta=(KeyGen^\beta,Sign^\beta,Verify^\beta)を署名スキームとする。
またランダムオラクルの定義は以下。
H:\{0,1\}^l\rightarrow \{0,1\}^kが以下を満たす時Hをランダムオラクルと呼ぶ。
1.過去に定めたH(x)は一意に決定され
2.H(x)が未定義のときには\{0,1\}^kからランダムに値を決める。
("デジタル署名の証明可能安全性"より)
定理の証明では、攻撃者と挑戦者の間のゲームを想定する。
このゲームでは、「挑戦者が用意した署名値」を攻撃者が偽造しようとする。(暗号系の安全性検証)
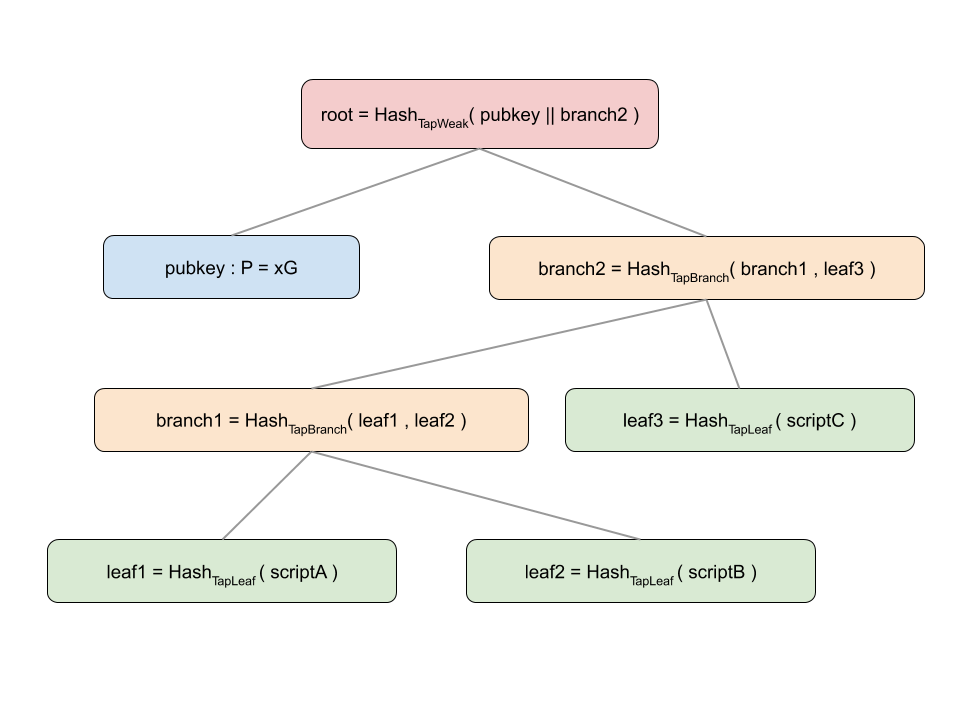
Taprootのアルゴリズムにおける公開鍵
下図のrootの値をtとして公開鍵Q=P+tG
ただしhash_{tag}(m)=SHA256(SHA256(tag)\|SHA256(tag)\|m)
安全性の証明におけるアルゴリズムの定義
TR^\betaと記述される\betaのTaprootを以下4つのアルゴリズムとして定義する。
1 鍵生成
KeyGen(b)はbit-bを入力して、keypair(sk_0,sk_1,pk)を出力する。
まず、sk^\alpha\xleftarrow{\char36 }\mathbb{Z}/p(\lambda)\mathbb{Z}を選択し、
pk^\alpha\xleftarrow{\char36 }sk^\alpha{G(\lambda)}を計算する。
もしb=0ならば、アウトプットは(sk^\alpha,\bot,pk^\alpha)
もしb=1ならば、(sk^\beta,pk^\beta)\leftarrow KeyGen^\betaで
\varepsilon\leftarrow H^{pk}(pk^\beta\|pk^\alpha)
このときアウトプットsk_0\leftarrow sk^\alpha + \varepsilon\\sk_1=(sk^\beta,pk^\alpha,pk^\beta)\\pk\leftarrow pk^\alpha+\varepsilon G
2 署名出力1
Sign^1(sk_0,m)は秘密鍵sk_0,メッセージmを入力しアウトプットである署名\sigmaを以下のように出力する。
k\xleftarrow{\char36 }\mathbb{Z}/p(\lambda)\mathbb{Z}\\R\leftarrow kG\\pk\leftarrow sk_0G\\e\leftarrow H^m(pk\|R\|m)を計算し \sigma=(R,k+esk_0)を出力する。
3 署名出力2
Sign^2(sk_1=(sk^\beta,pk^\alpha,pk^\beta),m)は秘密鍵sk_1,メッセージmを入力し、署名\sigmaを以下のように出力する。 \sigma^\beta=Sign^\beta(sk^\beta,m)を計算し、\sigma=(pk^\alpha,pk^\beta,\sigma^\beta)を出力する。
4 検証
Verify(pk,\sigma,m)は公開鍵pk,署名\sigma,メッセージmを入力しbitbを以下のように出力する。
もし\sigma=(R,s)ならばe\leftarrow H^m(pk\|R\|m)を計算し、sG=R+epkのときに限り受諾する。 もし\sigma=(pk^\alpha,pk^\beta,\sigma^\beta)ならば、まず pk=pk^\alpha+H^{pk}(pk^\beta\|pk^\alpha)Gを確認し、もしそうならば、Verify^\beta(pk^\beta,\sigma^\beta,m)のときに限り受諾する。
定理
定理1
もし離散対数問題が\mathscr{G}において困難かつ、\betaが偽造不可能ならば、TR^\betaは敵対者\mathscr{A}と挑戦者\mathscr{C}の間で以下のゲームにおいて偽造不可能である。
ゲーム
敵対者\mathscr{A}が bitbを選び、挑戦者\mathscr{C}に送信する。\mathscr{C}はKeyGen(b)により生成された公開鍵pkを返す。
\mathscr{A}は、 i\in \{1,2,...,q\},\lambdaについての多項式で拘束されるqに対して定義される署名クエリ(b_i,m_i)を送信する。 \mathscr{C}はSign^bにより生成される有効な署名\sigma_iを返す。
\mathscr{A}はVerify(pk,\sigma_*,m_*)が受諾されるような署名(\sigma_*,m_*)を再送する。
もし\betaが存在的偽造不可能(existentially unforgeable)ならば全てのiに対して(\sigma_*,m_*)≠(\sigma_i,m_i)を得る。 そうでなければ全てのiに対してm_*≠m_iを得られる。
解説
要するに、攻撃者はTaprootの鍵パスとスクリプトパスそれぞれについて、セキュリティパラメータが許す限りいくらでも事前に任意のメッセージに対する有効な署名を入手できる。この得られた有効な署名の情報を使って新しい有効な署名を作り出すことができれば攻撃者が勝利する。
ただし、新しい有効な署名はこれまでに得られたメッセージと署名のペアをそのまま提出してはならない。また、存在的偽造不可能でない場合は、メッセージだけを改変して署名を偽造することもできないはずである。
証明
この定理の証明は2つの補題からなる。
安全性の証明では以下のような方法が使われることに注意せよ。
暗号方式が用いられるときに妥当な情報を入手できる攻撃者が、
攻撃に成功したときに矛盾が生じることを示すやり方が用いられる。
http://www.tj.chiba-u.jp/~wkishi/cryptography.htmlhttp://www.tj.chiba-u.jp/~wkishi/cryptography.html
補題1
敵対者\mathscr{A}が確率\varepsilonでSign^2の形で偽造をアウトプットするならば、確率\varepsilon - neg(\lambda,q)で\betaの偽造を生成できる。
補題1の証明
\beta-挑戦者にアクセスできる挑戦者\mathscr{C}、敵対者\mathscr{A}の存在を仮定する。
まず\mathscr{C}は全てのランダムオラクルクエリに一様に独立に返答する。
\mathscr{C}は独立でランダムな鍵ペア(sk^\alpha,pk^\alpha)を選択する。
・もしb=0ならば、\mathscr{C}はpk^\alpha を\mathscr{A}に送信しsk=sk^\alphaと保存する。
・もしb=1ならば、\mathscr{C}は公開鍵pk^\betaを\beta挑戦者に要求し、pk=pk^\alpha +H^{pk}(pk^\beta\|pk^\alpha)Gを計算し、\mathscr{A}に送信する。
\mathscr{C}はsk=sk^\alpha +H^{pk}(pk^\beta\|pk^\alpha)と保存する。
署名クエリ(b_i,m_i)が与えられると、\mathscr{A}は以下のように振る舞う。
もしb_i=0ならばSign^1(sk,m_i)を実行し\sigma_iを返す。
もしb_i=1かつb=0ならば\botを返す。
もしb_i=1かつb=1ならば\beta挑戦者にm_iの問い合わせをして\sigma^\beta_Iを獲得し、\sigma_i=(pk^\alpha,pk^\beta,\sigma^\beta)を返答する。
最後に\mathscr{A}はSign^2の形で\sigma_*=(pk^\alpha_*,pk^\beta_*,\sigma^\beta_*)を満たす署名(\sigma_*,m_*)を返す。
更に、\sigma^\beta_*は鍵pk^\beta_*とpk=pk^\alpha_* +H^{pk}(pk^\beta_*\|pk^\alpha_*)Gと共にm_*に有効な署名となる。
まず、H^{pk}がランダムオラクルとしてモデリングされ、\mathscr{A}は多項式回問い合わせすることより(pk^\alpha_*,pk^\beta_*)=(pk^\alpha,pk^\beta)がごく僅かな確率を除いて成り立つ。
ゆえに、
(\sigma,m_*)がTR^\beta_*の偽造であるときに限り(\sigma^\beta_*,m_*)が\betaの偽造となるように、\sigma^\beta_*=\sigma^\beta_iのときに限り\sigma_*=\sigma_iが成り立つ。
補題2
敵対者\mathscr{A}が確率\varepsilonでSign^1の形で偽造をアウトプットするならば、確率\varepsilon - neg(\lambda,q)で(\mathscr{G},G,H^m)でのシュノア署名の偽造を生成できる。
補題2の証明
\mathscr{C}は以下のように振る舞う。
まず、ランダムオラクルH^Sへのアクセスでき、s=R+eP,P=H^S(P\|R\|m)を満たす署名(s,R)を期待するシュノア署名への挑戦者\mathscr{S}にアクセスできる。
\beta挑戦者にアクセスできる敵対者\mathscr{A}の存在を仮定する。
まず\mathscr{C}は全てのランダムオラクルクエリに一様に独立に返答する。
もしb=0ならば\mathscr{C}は\mathscr{S}から\mathscr{A}に公開鍵を転送し、全てのb_i=1の署名に\botを返し、
それ以外の場合には、全ての署名を\mathscr{S}に、H^mのクエリをH^Sに転送し、得られた偽造をシュノア偽造として提示する。
Sign^1(sk,m_i)を実行し\sigma_iを返す。
もしb_i=1かつb=0ならば\botを返す。
このとき証明はすぐに得られるので、以下b=1の場合の証明を行う。
\mathscr{C}は\mathscr{S}から公開鍵pk^\alphaを得られ、(sk^\beta,pk^\beta)\leftarrow KeyGen^\betaを選び、pk=pk^\alpha +H^{pk}(pk^\beta\|pk^\alpha)Gを計算する。\mathscr{C}は\mathscr{A}にpkを送信する。
\mathscr{C}はH^{pk}クエリに一様にランダムに返答する。\mathscr{C}はpkをpk^\alphaに置き換えてH^{m}クエリに返答する。その逆の場合はH^{S}クエリに転送する。
\mathscr{C}は署名クエリ(b_i,m_i)に以下のように返答する。
もしb_i=1ならば\mathscr{C}はSign^2の形で\sigma_i\leftarrow Sign^2 ((sk^\beta,pk^\alpha,pk^\beta),m_i)を得られ、返す。
もしb_i=0ならば\mathscr{C}は\mathscr{S}からm_iに関する署名(s_i,R_i)を要求する。
e_i=H^S(pk^\alpha\|R\|m_i)として、\mathscr{C}はe_iH^{pk}(pk^\beta\|pk^\alpha)をs_iに加えs_i^\primeを得られ、\sigma_i=(s_i^\prime,R_i)を返答する。
s_i^\prime G=s_iG+e_iH^{pk}(pk^\beta\|pk^\alpha)G\\=R_i+e_i(pk^\alpha +H^{pk}(pk^\beta\|pk^\alpha)G)\\=R_i+e_ipk
より、
\sigma_iは有効な署名となる。
しかし\mathscr{C}のH^mへの返答により、e_i=H^S(pk^\alpha\|R\|m_i)=H^m(pk\|R\|m_i)が保証され、これはTR^\betaの検証式となる。
\mathscr{A}はSign^1の形で\forall i,(\sigma_*,m_*)≠(\sigma_i,m_i)を満たす偽造(\sigma_*,m_*)を返し、Verify(pk,\sigma_*,m_*)を受諾する。
(s_*-e_*H^{pk}(pk^\beta\|pk^\alpha))G\\=R_*+e_*pk-H^{pk}(pk^\beta\|pk^\alpha)G\\=R_*+e_*pk^\alphaから(s_*-e_*H^{pk}(pk^\beta\|pk^\alpha),R_*)が有効なシュノア署名で、\mathscr{S}に対する署名クエリの出力と等しくない。
まとめ
補題1と補題2より、鍵パスとスクリプトパスどちらのケースであっても、定理1で偽造ができてしまうとシュノア署名自体の偽造ができてしまうことが分かる。したがって、Taprootの署名スキームはシュノア署名のスキーム自体と同程度に安全である。
感想
補題1,2両方とも敵対者の行動が不必要に制限されているように見え、本当にこの証明で安全性が示せているのかは疑問に感じた。
参考文献
https://github.com/apoelstra/taproot/blob/master/main.pdf
https://www.ieice.org/~isec/event/isec050517/isec05051703.pdf