Universal Arguments：証明システムの構成

Table of Contents

この記事はBlockchain Advent Calendar 2022 23日目の記事です。

※ブロックチェーンとはあまり関係がないような気もしますが、一応背景を説明するとこの論文で提案された証明システムは段階的検証可能計算(Incrementally verifiable computation )というアルゴリズムの論文で基礎として使われている証明系です。段階的検証可能計算はProof of necessary workで使われており、類似の「知識証明プロトコルを使った高速ブロックチェーン同期」は開発も活発でホットな分野なので、一応その辺りが繋がっています。

はじめに

本稿では[1]で提案されたuniversal argumentsと呼ばれる証明システムについて解説します。この証明システムは検証者による証明の検証が証明者の知識の長さに依存しない時間で行えます。つまり証明システムの実行やメッセージのやり取りが証明したい問題が属する集合に依存せず、証明したい問題自体の長さにのみ依存するような多項式で抑えられます。証明したい問題が属する集合はクラスNPに属する任意の集合を仮定しています。

Universal argumentsの定義

universal argumentsとは以下の性質を満たすstrategyの組 $(P, V)$ のことです。（Pは証明者、Vは検証者を表しています。） $R_u$ を正しいメッセージ $x$ とその証拠 $w$ とそれを受理する機械(チューリングマシン) $M$ 、 $M$ の最大の計算時間 $t$ の組 $((M, x, t), w)$ の集合、 $S_u$ を $R_u$ の要素の第1成分 $(M, x, t)$ の集合(つまり、正しいメッセージと機械、計算時間の組の集合)とします。

効率の良い検証(Efficient Verification)

ある多項式 $p$ が存在して任意の入力 $y=(M, x, t)$ に対して $V$ の計算時間が $p(|y|)$ 以下となる。

メッセージの長さの多項式時間で検証を行えるという意味です。特にプロトコルの全てのやり取りのメッセージの長さが $p(|y|)$ 以下となります。

相対的に効率の良い証明者による完全性(Completeness via a relatively-efficient prover)

$R_u$ の全ての要素 $((M, x, t), w)$ に対して $Pr[(P(w), V)(M, x, t)=1]=1$ が成り立つ。
さらにある多項式 $p$ が存在して証明者 $P(w)$ の入力 $(M, x, t)$ に対する計算時間は $p(|M|+T_M(x, w))\leq p(|M|+t)$ で抑えられる。

完全性が成り立つことに加えて証明者が証明中のチューリングマシンの計算時間を考慮したときに効率良く行えるということです。

計算量的健全性(Computational soundness)

$S_u$ に含まれない $(M, x, t)$ についてどんな多項式サイズの回路族 $\{ \tilde{P_n} \}_n$ に対しても無視できる関数(negligible function) $\mu$ を用いて $Pr[(P(w), V)(M, x, t)=1]< \mu (n)$ が成り立つ。

証明が正しくないなら証明者は効率の良い証明によって検証者を納得させられないという意味です。

弱い知識証明の性質(A weak proof-of-knowledge property)

任意の多項式 $p$ に対して多項式 $p'$ と確率的な多項式時間のオラクルマシン $E$ が存在して以下を満たす。
「任意の回路族 $\{ \tilde{P_n}\}_n$ と十分に長い $y=(M, x, t)$ に対して
$Pr[(P(w), V)(M, x, t)=1]>1/p(|y|)$ ならば「ある $y$ の証拠 $w$ が存在して、全ての $1\leq i\leq |w|$ に対して $E_{r}^{\tilde{P_n}}(y, i)=w_i$ 」となる確率が $1/p'(|y|)$ より大きくなる。」

ある程度の確率で証明者に受け入れられる証明についてはその確率に応じた確率でその証明者が持つ知識を証明から得ることができるということです。

PCP system

Universal argumentsの構成にはPCPシステムを用います。PCPシステムについては[2]の記事で解説されています。文字列 $x$ と文字列の集合 $S$ に対して $x\in S$ を証明するとします。 $S\in \text{Ntime}(t(\cdot))$ であり、 $S$ に対応した $(x, w) \in R$ と $x\in S$ が同値となるような多項式時間決定可能な関係 $R$ が存在する場合を考えます。この場合には通常のPCPの性質である完全性と健全性に加えて以下の良い性質を持つPCPシステムを構成できます。Universal argumentsの構成のためにはこれらの性質が重要です。

比較的効率の良いオラクルの構成(Relatively-efficient oracle-construction)

多項式アルゴリズム $P$ であってどんな $(x,w)\in R$ に対しても $V$ が必ず受け入れるようなオラクル $\pi _x$ を出力するものが存在する。

多項式時間の証明者によって完全性が満たされる、という意味です。

適応的でない検証者(Non-adaptive verifier)

$V$ を $Q$ と $D$ の二つのアルゴリズムに分割できて、複数回行われる $Q$ の入力は他の $Q$ の出力に依存せず、これらの $Q$ の出力を用いて $D$ によって受け入れるかどうかを判定する。

検証者が行うオラクルへのアクセスがそれまでのオラクルのアクセスによらずに行われるという意味です。検証者は前までのクエリーに対する証明者の返答に応じて後のクエリーを変えることができないという意味です。

効率の良い逆サンプリング(Efficient reverse-sampling):

確率的多項式アルゴリズム $S$ であってどんな $x$ と整数 $i,j$ に対しても $Q(x, r, i) = j$ を満たすような $r$ を出力するものが存在する。

検証者がクエリーを作るために使う乱数をクエリーから求め直す効率の良いアルゴリズムが存在するという意味です。

知識証明の性質(A proof-of-knowledge property)

確率的多項式時間のオラクルマシン $E$ であって $V^\pi$ が $x$ を受け入れる確率が（ $x$ の長さに対して）十分大きいならば $(x, w)\in R$ と $Pr[E^\pi (x, i)=w_i]>2/3$ を満たす $w = w_1,\cdots w_t$ が存在する。

ある程度の確率で証明者に受け入れられる証明については $2/3$ より大きな確率で証明者のみが持つ知識を証明から得ることができるということです。弱い知識証明の性質(A weak proof-of-knowledge property)とは異なり知識を証明から得る確率は $2/3$ より大きな確率になっています。

Universal argumentsの構成

さらに無視できる確率でしか衝突の起こらないハッシュ関数の族 $\{ h_{\alpha} \}$ の存在を仮定します。するとuniversal argumentsを以下のように具体的に構成できます。

$y=(M, x, t)$ を $P$ と $V$ に共通の入力、 $(y, w)\in R_u$ を満たす $w$ を $P$ のみの入力として $P$ が $y \in S_u$ を証明するとします。これらは上で述べた良い性質を満たす条件を満たしていて、性質の中で述べたアルゴリズムを同じ記号を用いて $P_{pcp}, Q_{pcp}, D_{pcp}, S_{pcp}, E_{pcp}$ とします。

つまり

$P_{PCP}$ :証明者のアルゴリズム。
$Q_{PCP}, D_{PCP}$ :検証者のアルゴリズム。入力 $x$ と乱数 $r$ に基づいてクエリー $b_1, \cdots b_{p(|x|)} :=Q_{PCP}(x, r, 1), \cdots Q_{PCP}(x, r, p(|x|)) (p$ は固定された多項式)をもとめ、 $D_{PCP}(x, r, b_1, \cdots b_{p(|x|)})$ によって検証結果を判定する。
$S_{pcp}$ :効率の良い逆サンプリング(Efficient reverse-sampling)の中の乱数を求める確率多項式アルゴリズム。どんな $x$ と整数 $i,j$ に対しても $Q_{PCP}(x, r, i) = j$ を満たすような $r$ を出力する。
$E_{pcp}$ :知識証明の性質(A proof-of-knowledge property)の中の確率多項式時間のオラクルマシンのアルゴリズム。検証者が $x$ を受け入れる確率が（ $x$ の長さに対して）十分大きいならば $(x, w)\in R$ と $Pr[E_{pcp}^\pi (x, i)=w_i]>2/3$ を満たす。
とします。これらを用いて以下のようにuniversal argumentsの証明システムを構成します。
V1:
ランダムに選択した $\alpha \in \{ 0,1\} ^n$ を $P$ に送ります。
P1:
1. 前準備として $M(x, w)$ の計算時間 $t'$ を計算し、, $w'=(w, 1^{t'})$ とします。
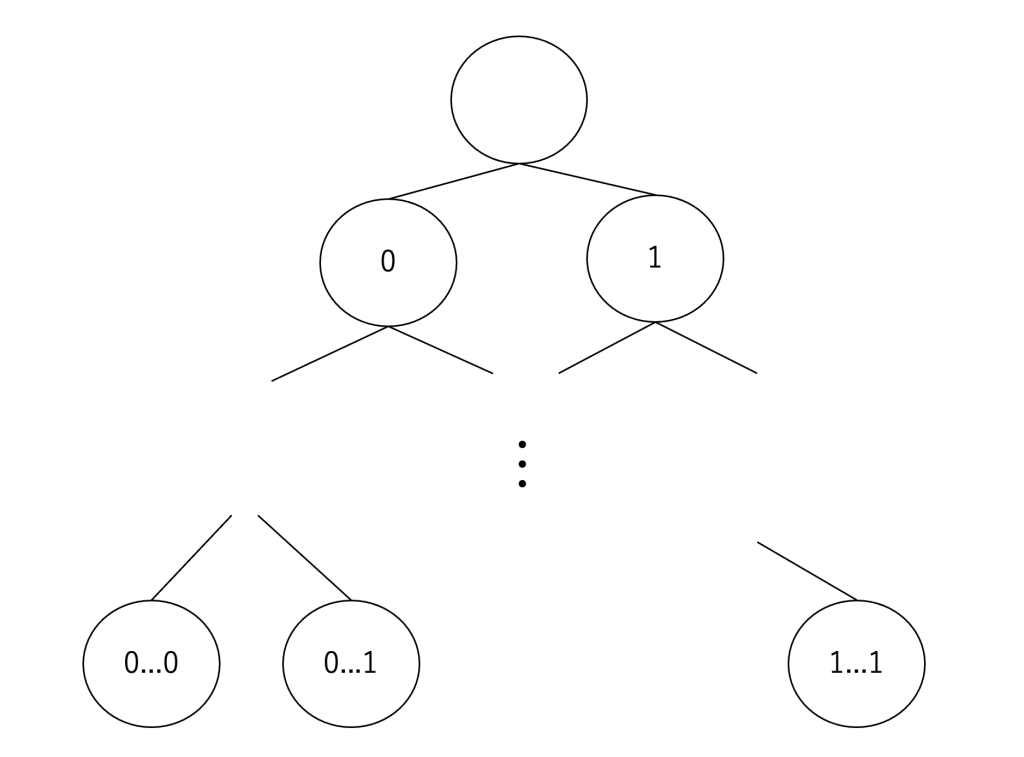
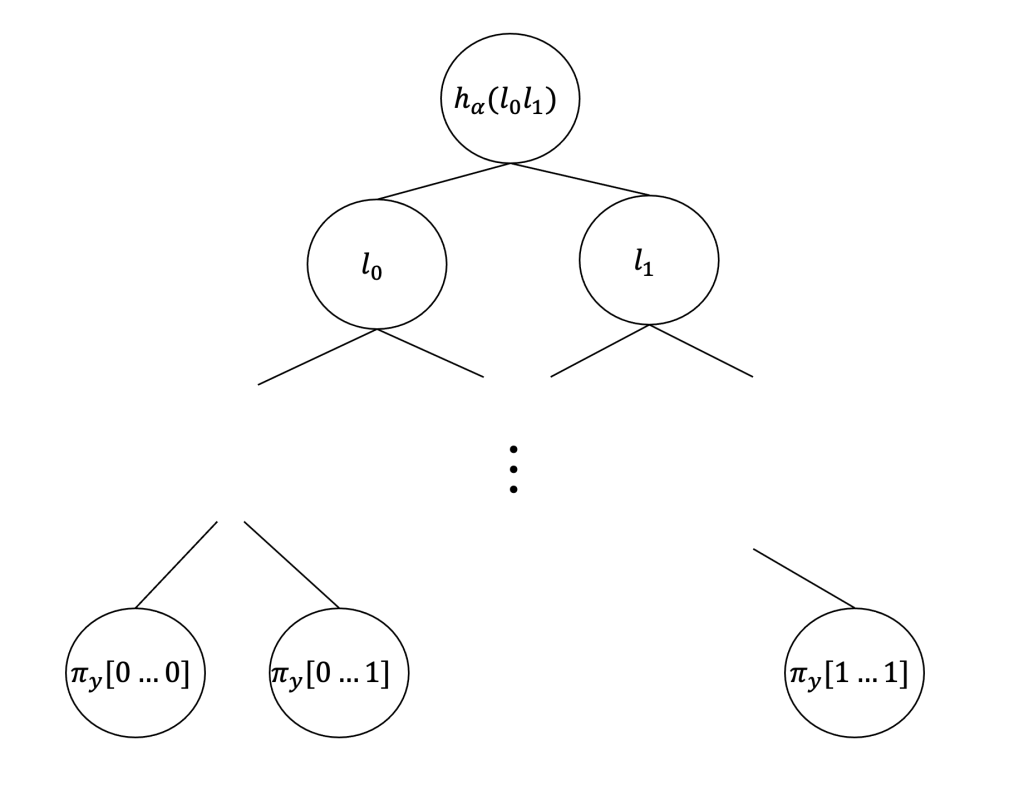
2. オラクル $\pi _y = P_{pcp}(y, w')$ を構成して長さを $d=\log_2 |\pi _y|$ とします。
3. ハッシュ木を以下のように構成します。このハッシュ木は二分木で下図の様な別の(0と1から成る)文字列の二分木と各頂点が一対一に対応しています。文字列の木の\gammaと対応するハッシュ木の頂点をl_{\gamma}と表します。
  - $\gamma$ が文字列の木の葉のとき $\gamma$ は $d$ の文字列で、対応するハッシュ木の葉 $l_{\gamma}$ は $\pi _y$ の $\gamma$ の位置にある文字です。
  - $\gamma$ が文字列の木の葉以外の頂点のとき $\gamma$ は $d$ 未満の文字列で、対応するハッシュ木の頂点 $l_{\gamma}$ は $h_{\alpha}(\gamma 0\gamma 1)$ です。
4. 3で構成したハッシュ木の根を $l_{\lambda}$ として $(d, l_{\lambda})$ を送ります。
  
  文字列の木
  
  構成したハッシュ木
V2:
PCPシステムのためのランダム値 $r$ を送ります。
P2:
P1で構成したハッシュ木と合わせて知識wの証明となるような返答を以下の様に返します。
1. $Q_{pcp}$ とランダム値 $r$ を用いて $\pi _y$ に対するクエリーの入力 $q_i=Q_{pcp}(y, r, i)$ を $1\leq i\leq m$ について求めます（ $m$ はPCPシステムのクエリーの数）。
2. $1\leq i\leq m, 0\leq j\leq d-1$ についてハッシュ木の頂点 $(l_{\gamma_{i,j}0},l_{\gamma_{i,j}1} )$ を送る。
V3:
P2の返答がPCPシステムの証明、P1のメッセージと矛盾がないかどうかを以下のように検証します。P2で受け取った文字列の木の\gammaと対応するハッシュ木の頂点をl'_{\gamma}と表します。
1. PCPシステムの証明と矛盾がないかどうかを検証します。
  ハッシュ木の葉は長さ $d$ の文字列と対応しておりその文字列の位置にある $\pi _y$ の文字となっているはずです。つまり $Q_{pcp}$ を用いて、 $\pi _y$ に対するクエリーの入力 $q_i=Q_{pcp}(y, r, i)\;(1\leq i\leq m)$ を求めると証明が正しければ $D_{pcp}(y, r,l'_{q_1}\cdots l'_{q_m})=1$ が成り立つはずなのでこれを検証します。
2. P1のメッセージと矛盾がないかどうかを検証します。
  これは $1\leq i\leq m, 0\leq j\leq d-1$ について $l'_{\gamma_{i,j}0}=h(l'_{\gamma_{i,j}0}l'_{\gamma_{i,j}1})$ が成り立つかどうかを葉から順に確かめていき、最後に $l_{\lambda}=h(l'_{0}l'_{1})$ を確かめることで検証できます。ハッシュ関数 $h_{\alpha}$ の衝突が生じる確率が低いことから、この検証を通過すれば $P$ が正しい知識 $w$ を持っている確率が高いことが分かります。