この記事で紹介する内容
計算複雑性理論に属する P 問題と NP 問題とを調べ、それらの関係がどのように暗号資産に影響するかを紹介する。
参考
https://drops.dagstuhl.de/opus/volltexte/2017/8162/pdf/LIPIcs-ITCS-2017-60.pdf
M.Sipser Introduction to the Theory of Computation section 7
計算複雑性理論
あるアルゴリズムへの入力データの大きさを増やしたとき、出力に必要な空間量や実行時間がどのように増えるのかを扱う理論。
複雑性クラス
計算複雑性理論において問題をその複雑さからクラス分けした集合のこと。以下に今回扱う複雑性クラスを示す。
P 問題
- 判定問題のうち、ある決定性チューリングマシンによって多項式時間で解かれるものの全体
yes/no で答えられる問題があり、解が一意に決まるアルゴリズムによって多項式時間で判定できる問題。
例としてグラフ理論におけるオイラー閉路の存在を判定する問題は頂点数 V、 辺の数 E として O(V + E) で計算できる。
NP 問題
- 非決定性チューリングマシンによって多項式時間で解くことができる問題
- yes となる証拠が与えられたとき、その証拠が本当に正しいかどうかを多項式時間で判定できる問題
解を求めるのに効率的な選択が毎回可能なアルゴリズムによって多項式時間で判定できる、または yes である証拠があった場合に、その証拠が正しいかどうか多項式時間で判定できる問題。
例として SAT と呼ばれる論理式の充足可能性を判定する問題があり、変数の数を N とすると決定性チューリングマシンで解く場合は O(2^N)、非決定性チューリングマシンで解く場合は O(N) で計算できる。
NP 困難
- 問題が「
NPに属する任意の問題と比べて、少なくとも同等以上に難しい」こと - 問題
HがNP困難であるとは、NPに属する任意の問題LがHへ多項式時間で帰着可能であること
問題が NP に属しているかは不明であるが、少なくとも同等以上に難しい問題。
NP 完全
- クラス
NPに属する決定問題かつ任意のクラスNPに属する問題から多項式時間還元(帰着)可能なもののこと
NP かつ、NP 困難である問題。
前述の SAT は NP 完全な問題の一つである。
それぞれの集合の関係
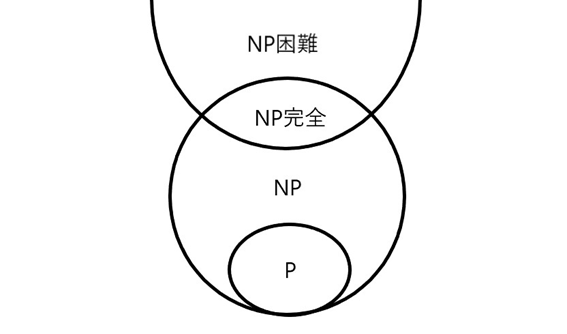
P≠NP
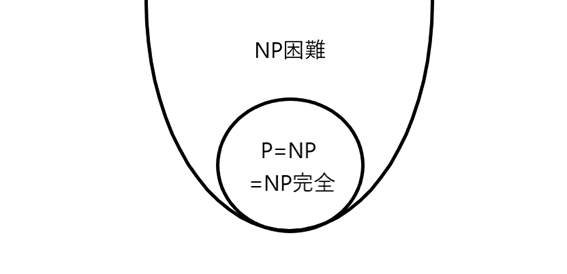
P=NP
P と NP の違い
何を用いて問題を解くか
-
P問題では決定的チューリングマシン
ある入力をしたときに計算機がどのような動作をするかが一意に決まっている。
例として現在のコンピュータ。 -
NP問題では非決定的チューリングマシン
ある入力をしたときに計算機が複数の動作を同時にとれ、解へ近づくのに最も効率的な選択を毎回できる。
未だ理論段階。
NP 問題を決定的チューリングマシンで解こうとする場合、指数時間になってしまう可能性がある。
PvsNP 問題
P 問題と NP 問題が同じ集合であるのか、異なる集合であるのかという問題。
P \neq NP であるという予想が一般的だが、証明はいまだされていない。
P \neq NP であることを解決するためには、NP 問題すべてが P 問題として解ける(すなわち、NP 完全な問題が P 問題として解ける)、もしくは NP 問題の中には P 問題としては解けないものがあるということを証明しなければならない。
多項式的に結ばれた関係 R
R \in \{0,1\}^*×\{0,1\}^*、R(x) = \{ y \mid (x, y) \in R \} とする。
任意の x \in \{0,1\}^* に対して、ある定数 c が存在して、
R(x) \subseteq \{0,1\}^{|x|^c} であるとき、関係 R を多項式的に結ばれた関係と呼ぶ。
R は、あるインスタンス x が与えられたときに、(x, y) \in R となるような解 y を効率的に見つけられるかどうかという探索問題と結びついている。
多項式的に結ばれた関係 R と複雑性クラス
探索問題のクラスとしてのクラス P
与えられたインスタンス x から、(x, y) \in R となる y を見つけるか、またはそのような y が存在しないことを与える多項式アルゴリズムと R の探索問題にクラス P は対応している。
与えられたグラフに対してオイラー閉路の一つを見つける問題が例として挙げられる。
探索問題のクラスとしてのクラス NP
与えられたインスタンス x と解 y のペアが与えられたとき、(x, y) \in R であるかどうかを決定する多項式時間アルゴリズムが存在する場合の多項式で結ばれた関係 R を NP-relation という。
クラス NP は NP-relation の探索問題のクラスに対応しており、FNP、TFNP 等のクラスがある。
SAT の解を求める問題が例として挙げられる。
探索問題と PvsNP 問題
PvsNP 問題を探索問題から扱うと、任意の NP-relation の探索問題が多項式時間で解けるかどうかとなる
P = NP の場合
与えられたインスタンス x と解 y のペアが (x,y) \in R であるかどうかを容易に検証できる場合、その解 y をインスタンス x のみが与えられた場合に容易に解決することができることを意味する。
これはすなわち、すべての NP-relation の探索問題が容易に解けることを意味する。
P ≠ NP の場合
P \neq NPであるならば、ある NP-relation の探索問題は容易に解けるが、容易に解くことができない(= 指数時間以上かかる)問題が存在することを意味する。
NP 完全と探索問題
還元
還元とは、ある計算問題(探索問題または決定問題のいずれか)を、別の計算問題(これも探索問題または決定問題のいずれか)に対するサブルーチンの呼び出しを用いて解決するものであり、効率的な(つまり多項式時間の削減)を目的とした還元を特に Cook 還元と呼ぶ。
決定問題を決定問題に還元することが一般的であるが、探索問題を探索問題に、探索問題を決定問題に還元することも可能であり、一例として NP-relation の探索問題を、あるNP集合の要素を決める決定問題へと還元することが挙げられる。
探索問題から決定問題への還元
NP-relation R に対して、L_R = \{ x \mid R(x) \neq \empty \} と定義する。
ある問題(言語)Lに対して、L = L_R となる NP-relationRが存在する(すなわち、多項式時間で解の検証が可能なRが存在する)時、探索問題は決定問題に(自己)還元可能という。
別の定義としてオラクルを用いて入力長の多項式時間で再帰的に決定するものも存在するが、やや煩雑なため割愛する。
NP 完全
NP 完全の集合に対応するすべての NP-relation の探索問題は、自己還元可能である。
従って、ある二項関係が NP-relation であり、すべての NP-relation がそれに還元可能である場合、その二項関係は NP 完全となる。
しかしこのようなNP完全を定義したというだけでは、そのことを満たす対象が存在することを示す訳ではない。
暗号化技術への影響
鍵という証拠があった場合、復元化は決定的チューリングマシンであっても多項式時間で可能ではあるが、盗聴した暗号文を復元することは今のところ多項式時間ではできない。
しかし P = NP であった場合、決定的チューリングマシンで暗号文を多項式時間で解くことが可能なアルゴリズムが存在する可能性がある。その場合、既存のコンピュータでも暗号復元が可能となるため暗号資産のセキュリティが崩壊してしまう。ただし、そのような証明が構成的な方法であり、かつオーバーヘッドも現実的に計算可能な場合である必要があり、また量子暗号については安全ではないかと考えられている。
また非決定的チューリングマシンが実現した場合も同様に、暗号文を多項式時間で解くことが可能となるため暗号資産のセキュリティは崩壊してしまう。
非決定的チューリングマシンを用いることで NP 問題を解決することができるのでは、と期待されているが、そもそも仮に P \neq NP であるとすると非決定的チューリングマシンは実際には実装することができないかもしれないという考えもある。


